Question

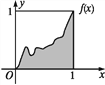
【题目】设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S.先产生两组(每组N个)0~1区间上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为_____.

Answer 1

【答案】

【解析】由0≤f(x)≤1可知曲线y=f(x)与直线x=0,x=1,y=0围成了一个曲边图形.

因为产生的随机数对在题图的正方形内,正方形的面积为1,共有N对数,即有N个点,且满足yi≤f(xi)(i=1,2,…,N)的有N1个点,即在函数f(x)图象上及下方有N1个点,所以由几何概型的求概率公式得:曲线y=f(x)与x=0,x=1,y=0围成的面积的近似值为×1=.