题目内容
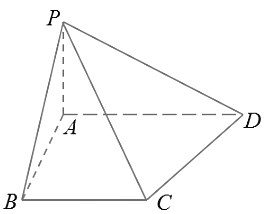
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,且AD∥BC,AD⊥CD,∠ABC=60°,BC=2AD=2,PC=3,△PAB是正三角形.
(1)求证:AB⊥PC;
(2)求二面角P﹣CD﹣B的平面角的正切值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要证线线垂直,先证线面垂直,由于![]() 是正三角形,取
是正三角形,取![]() 中点
中点![]() ,则有
,则有![]() ,从而只要再证
,从而只要再证![]() 即可证;
即可证;
(2)关键是作二面角的平面角,由(1)知平面![]() 平面
平面![]() ,因此只要作作PO⊥CE,PH⊥CD,连结OH,就可得∠PHO为二面角P﹣CD﹣B的平面角,接着就是计算出这个角即可.
,因此只要作作PO⊥CE,PH⊥CD,连结OH,就可得∠PHO为二面角P﹣CD﹣B的平面角,接着就是计算出这个角即可.
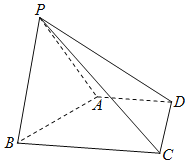
(1)证明:取AB中点E,连结PE,CE,
易证△ABC为正三角形,E为AB中点,∴CE⊥AB,
∵△ABP为正三角形,E为AB中点,∴PE⊥AB,
∴AB⊥平面PCE,
∴AB⊥PC.
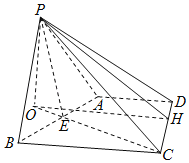
(2)解:过P点作PO⊥CE,PH⊥CD,连结OH,
∵AB⊥平面PCE,∴平面ABCD⊥平面PCE,
∵PO⊥CE,∴PO⊥平面ABCD,
∵PH⊥CD,∴OH⊥CD,
∴∠PHO为二面角P﹣CD﹣B的平面角,
四边形ABCD是直角梯形,且AD∥BC,AD⊥CD,
∠ABC=60°,BC=2AD=2,PC=3,△PAB是正三角形.
AB=2,PA=PB=2,PE=CE![]() ,∠PCE=30°,
,∠PCE=30°,
所以PO![]() ,OC
,OC![]() ,∠ECD=60°,OH
,∠ECD=60°,OH![]() ,
,
三角形POH是直角三角形,∠POH=90°,
∴![]() .
.
∴二面角P﹣CD﹣B的平面角的正切值:![]() .
.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 地区2019年足球特色学校的个数(精确到个)
地区2019年足球特色学校的个数(精确到个)
参考公式: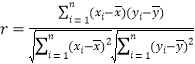 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.