题目内容

已知锐角△ABC中，角A、B、C的对边分别为a，b，c，且tanB=
3
ac
a2+c2-b2
求∠B．
分析：已知等式左边利用同角三角函数间的基本关系化简，右边变形后利用余弦定理化简，求出sinB的值，由B为锐角三角形的内角，利用特殊角的三角函数值即可求出B的度数．
解答：解：∵tanB=
sinB
cosB
，cosB=
a2+c2-b2
2ac
，tanB=
3
ac
a2+c2-b2
，
∴
sinB
cosB
=
3
2
a2+c2-b2
2ac
=
3
2
cosB
，
∴sinB=
3
2
，
∵B为锐角三角形的内角，
∴∠B=60°．
点评：此题考查了余弦定理，同角三角函数间的基本关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
已知锐角△ABC中，角A、B、C的对边分别为a，b，c，a=
2
，b=
3
，B=
π
3
．
（Ⅰ）求角A的大小；
（Ⅱ）设函数f(x)=cosB•sin2x+cos2x，当x∈[-
π
4
，0]时，求f（x）的值域．
已知锐角△ABC中的三个内角分别为A，B，C．
（1）设
BC
•
CA
=
CA
•
AB
，求证：△ABC是等腰三角形；
（2）设向量
s
=（2sinC，-
3
），
t
=（cos2C，2cos2
C
2
-1），且
s
∥
t
，若sinA=
2
3
，求sin（
π
3
-B）的值．
（2009•淮安模拟）已知锐角△ABC中内角A，B，C的对边分别为a，b，c，且c=6，向量
s
=（2sinC，-
3
），
t
=（cos2C，2cos2
C
2
-1），且
s
∥
t
．
（1）求C的大小；
（2）若sinA=
1
3
，求sin(
π
3
-B)的值．
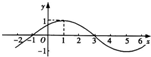已知函数f（x）=Asin（ωx+φ）（其中x∈R，A?＞0，ω＞0，-
π
2
＜φ＜
π
2
）的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）已知锐角△ABC中的三个内角分别为A，B，C，若有f（
A
π
）=
3
2
，边BC=
7
，sin B=
21
7
求△ABC的面积．
已知锐角△ABC中，三个内角为A，B，C，两向量
p
=（2-2sinA，cosA+sinA），
q
=（sinA-cosA，1+sinA），若
p
与
q
是共线向量．
（1）求∠A的大小；  
（2）求函数y=2sin2B+cos(
C-3B
2
)取最大值时，∠B的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网