题目内容
8．若x，y满足条件$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥0}\\{y≤a}\end{array}\right.$，且z=2x+3y的最大值是5，则实数a的值为1．分析 先画出可行域，结合图形分析出目标函数z=2x+3y取得最大值时对应点的坐标，把其代入目标函数再结合目标函数z=2x+3y的最大值为5，即可求出实数a的值．
解答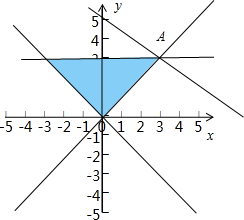 
解：实数x，y满足不等式组$\left\{\begin{array}{l}x-y≤0\\ x+y≥0\\ y≤a\end{array}\right.$，如图，
由图可知，当x=a，y=a时，
目标函数z=2x+3y的最大值是5．
5=2a+3a，解得：a=1
故答案为：1．
点评 本题主要考查简单线性规划的应用以及数形结合思想的应用．在求目标函数的最值时，一般是在可行域的特殊点处，所以一般在解选择和填空题时，常用特殊点代入法．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，E为PD中点．
3．已知log89=a，log25=b，则lg3=（ ）
| A． | $\frac{a}{b-1}$ | B． | $\frac{3}{2（b-1）}$ | C． | $\frac{3a}{2（b+1）}$ | D． | $\frac{3（a-1）}{2b}$ |
12．若角α的终边上有一点P（-1，m），且sinαcosα=$\frac{{\sqrt{3}}}{4}$，则m的值为（ ）
| A． | $\sqrt{3}$ | B． | $±\sqrt{3}$ | C． | $-\sqrt{3}$或$-\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{3}}}{4}$ |