题目内容
已知 、
、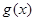 都是定义在R上的函数,
都是定义在R上的函数, ,
,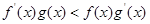 ,
,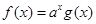 ,
, ,则关于x的方程
,则关于x的方程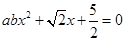 (
(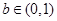 )有两个不同实根的概率为 .
)有两个不同实根的概率为 .
 、
、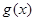 都是定义在R上的函数,
都是定义在R上的函数, ,
,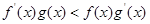 ,
,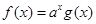 ,
, ,则关于x的方程
,则关于x的方程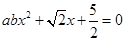 (
(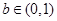 )有两个不同实根的概率为 .
)有两个不同实根的概率为 .
试题分析:∵
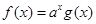 ,∴
,∴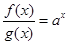 ,∵
,∵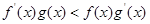 ,∴
,∴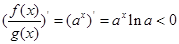 ,
,即
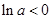 ,即
,即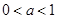 ,又∵
,又∵ ,∴
,∴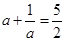 ,即
,即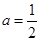 ,
,∵关于x的方程
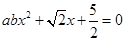 (
(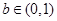 )有两个不同实根,∴
)有两个不同实根,∴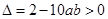 即
即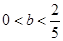 ,
,∴
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 、
、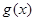 都是定义在R上的函数,
都是定义在R上的函数, ,
,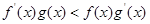 ,
,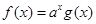 ,
, ,则关于x的方程
,则关于x的方程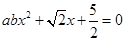 (
(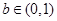 )有两个不同实根的概率为 .
)有两个不同实根的概率为 .
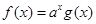 ,∴
,∴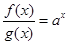 ,∵
,∵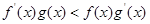 ,∴
,∴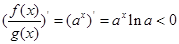 ,
,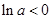 ,即
,即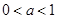 ,又∵
,又∵ ,∴
,∴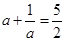 ,即
,即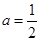 ,
,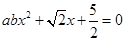 (
(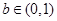 )有两个不同实根,∴
)有两个不同实根,∴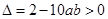 即
即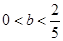 ,
, .
.
 阅读快车系列答案
阅读快车系列答案