题目内容
(本小题满分14分)
已知函数 对任意实数
对任意实数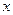 均有
均有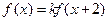 ,其中常数
,其中常数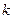 为负数,且
为负数,且 在区间
在区间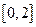 上有表达式
上有表达式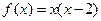 .
.
(1)求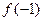 ,
,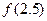 的值;
的值;
(2)写出 在
在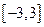 上的表达式,并讨论函数
上的表达式,并讨论函数 在
在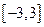 上的单调性;
上的单调性;
(3)求出 在
在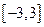 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
已知函数
 对任意实数
对任意实数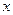 均有
均有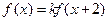 ,其中常数
,其中常数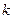 为负数,且
为负数,且 在区间
在区间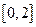 上有表达式
上有表达式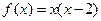 .
.(1)求
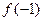 ,
,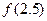 的值;
的值;(2)写出
 在
在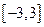 上的表达式,并讨论函数
上的表达式,并讨论函数 在
在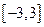 上的单调性;
上的单调性;(3)求出
 在
在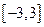 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.(1)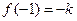 ,
,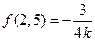
(2)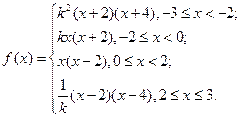
 在
在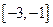 与
与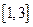 上为增函数,在
上为增函数,在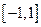 上为减函数;
上为减函数;
(3)① 而
而 在
在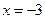 处取得最小值
处取得最小值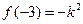 ,在
,在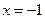 处取得最大值
处取得最大值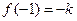 .
.
②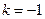 时,
时, 在
在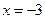 与
与 处取得最小值
处取得最小值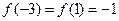 ,在
,在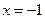 与
与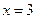 处取得最大值
处取得最大值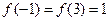 .
.
③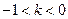 时,
时, 在
在 处取得最小值
处取得最小值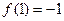 ,在
,在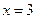 处取得最大值
处取得最大值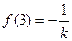 .
.
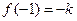 ,
,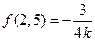
(2)
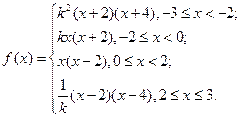
 在
在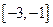 与
与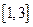 上为增函数,在
上为增函数,在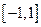 上为减函数;
上为减函数;(3)①
 而
而 在
在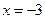 处取得最小值
处取得最小值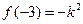 ,在
,在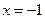 处取得最大值
处取得最大值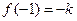 .
.②
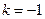 时,
时, 在
在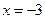 与
与 处取得最小值
处取得最小值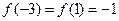 ,在
,在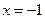 与
与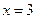 处取得最大值
处取得最大值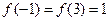 .
.③
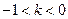 时,
时, 在
在 处取得最小值
处取得最小值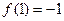 ,在
,在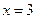 处取得最大值
处取得最大值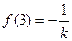 .
.本题主要考查了函数的基本性质,考查了分类讨论、函数与方程、数形结合数学思想方法,考查转化与化归的能力、逻辑推理能力。
(1)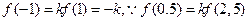 ,
,
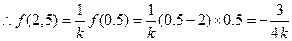 .
.
(2)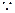 对任意实数
对任意实数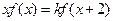 ,
,
 .
.
当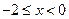 时,
时, ;
;
当 时,
时,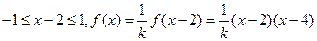 .
.
故
 在
在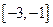 与
与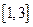 上为增函数,在
上为增函数,在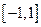 上为减函数;
上为减函数;
(3)由函数 在
在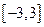 上的单调性可知,
上的单调性可知,
 在
在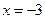 或
或 处取得最小值
处取得最小值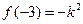 或
或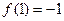 ,而在
,而在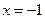 或
或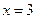 处取得最大值
处取得最大值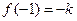 或
或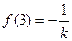 .
.
故有
① 而
而 在
在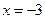 处取得最小值
处取得最小值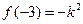 ,在
,在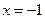 处取得最大值
处取得最大值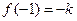 .
.
②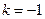 时,
时, 在
在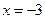 与
与 处取得最小值
处取得最小值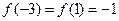 ,在
,在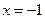 与
与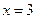 处取得最大值
处取得最大值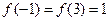 .
.
③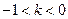 时,
时, 在
在 处取得最小值
处取得最小值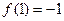 ,在
,在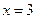 处取得最大值
处取得最大值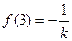 .
.
点评:函数基本性质的考查是高考热点问题之一,从近几年的高考看,函数问题是高考中的重点考查内容之一,分值近40分左右,主要是考查函数解析式、定义域、值域(最值、参数取值范围)、函数的图象、单调性、奇偶性等性质,考查的函数也是常见的二次函数、指数对数函数为主,但会将这几种函数结合起来、将抽象函数与具体函数结合起来的趋势,这种命题的趋势在今后几年内继续保持。
(1)
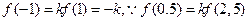 ,
,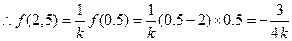 .
.(2)
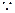 对任意实数
对任意实数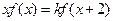 ,
, .
.当
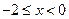 时,
时, ;
;当
 时,
时,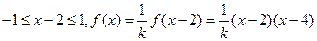 .
.故

 在
在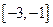 与
与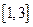 上为增函数,在
上为增函数,在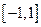 上为减函数;
上为减函数;(3)由函数
 在
在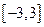 上的单调性可知,
上的单调性可知, 在
在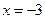 或
或 处取得最小值
处取得最小值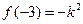 或
或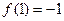 ,而在
,而在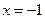 或
或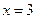 处取得最大值
处取得最大值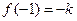 或
或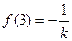 .
.故有
①
 而
而 在
在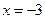 处取得最小值
处取得最小值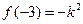 ,在
,在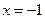 处取得最大值
处取得最大值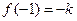 .
.②
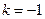 时,
时, 在
在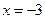 与
与 处取得最小值
处取得最小值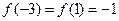 ,在
,在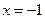 与
与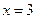 处取得最大值
处取得最大值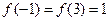 .
.③
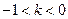 时,
时, 在
在 处取得最小值
处取得最小值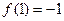 ,在
,在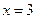 处取得最大值
处取得最大值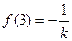 .
.点评:函数基本性质的考查是高考热点问题之一,从近几年的高考看,函数问题是高考中的重点考查内容之一,分值近40分左右,主要是考查函数解析式、定义域、值域(最值、参数取值范围)、函数的图象、单调性、奇偶性等性质,考查的函数也是常见的二次函数、指数对数函数为主,但会将这几种函数结合起来、将抽象函数与具体函数结合起来的趋势,这种命题的趋势在今后几年内继续保持。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
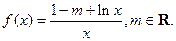
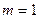 ,判断函数在定义域内的单调性
,判断函数在定义域内的单调性 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。 。
。 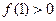 .
.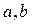 的值
的值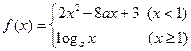 在
在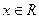 内单调递减,则
内单调递减,则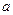 的范围是( )
的范围是( )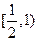
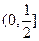
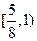
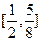
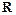 上的函数
上的函数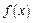 满足
满足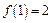 ,
,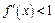 ,则不等式
,则不等式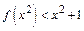 的解集为 .
的解集为 .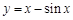 在
在 上是( )
上是( )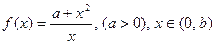 ,则下列判断正确的是( )
,则下列判断正确的是( )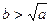 时,
时,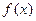 的最小值为
的最小值为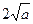 ;
; 时,
时, ;
;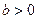 ,
,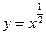
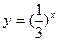
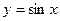

 上的函数
上的函数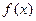 满足
满足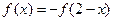 ,且当
,且当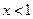 时
时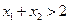 ,
,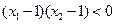 ,则
,则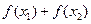 的值是
的值是