题目内容
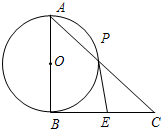
选修4-1：几何证明选讲如图，以Rt△ABC的一条直角边AB直径作圆O，交斜边AC于P点，过P点作圆O的切线交BC于E点．求证：BE=CE．
分析：由AB是圆O的直径可得BP⊥AC，由弦切角定理及切线的性质可知∠EPB=∠EBP=∠BAP，即证BE=PE，只要证明∠CPE=∠PCE，即正PE=CE，即可
解答：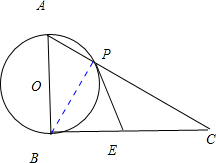
证明：连接BP，
∵AB是圆O的直径
由圆周角定理可得，BP⊥AC…（3分）
又∵EP、EB都是圆O的切线，
由切线的性质可得，∠EPB=∠EBP，且BE=PE
根据弦切角定理可知，∠EPB=∠BAP（6分）
又∠CPE+∠EPB=∠PCE+∠BAP=90°
∴∠CPE=∠PCE，
∴PE=CE
∴BE=CE…（10分）
证明：连接BP，∵AB是圆O的直径
由圆周角定理可得，BP⊥AC…（3分）
又∵EP、EB都是圆O的切线，
由切线的性质可得，∠EPB=∠EBP，且BE=PE
根据弦切角定理可知，∠EPB=∠BAP（6分）
又∠CPE+∠EPB=∠PCE+∠BAP=90°
∴∠CPE=∠PCE，
∴PE=CE
∴BE=CE…（10分）
点评：本题主要考查了圆的切线性质及弦切角定理的综合应用，解答此类问题的关键是灵活应用圆的性质
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
选修4-1：几何证明选讲
A、选修4-1：几何证明选讲 
选修4-1：几何证明选讲
（2012•徐州模拟）选修4-1：几何证明选讲
（2013•南京二模）选修4-1：几何证明选讲