题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的函数,记
上的函数,记![]() ,
,![]() 的最大值为
的最大值为![]() .若存在
.若存在![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,则称一次函数
,则称一次函数![]() 是
是![]() 的“逼近函数”此时的
的“逼近函数”此时的![]() 称为
称为![]() 在
在![]() 上的“逼近确界”.
上的“逼近确界”.
(1)验证![]() 是
是![]() ,
,![]() 的“逼近函数”;
的“逼近函数”;
(2)已知![]() ,
,![]() ,
,![]() .若
.若![]() 是
是![]() 的“逼近函数”,求a,b的值;
的“逼近函数”,求a,b的值;
(3)已知![]() ,
,![]() ,求证;对任意常数a,b,
,求证;对任意常数a,b,![]() .
.
【答案】(1)见解析;(2)a![]() .b
.b![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)记G(x)=2x2﹣(4x﹣1)=2(x﹣1)2﹣1,x∈[0,2].利用二次函数的单调性可得|G(x)|的最大值为1,且G(0)=1,G(1)=﹣1,G(2)=1.
(2)F(x)![]() (ax+b),由
(ax+b),由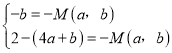 ,可得M(a,b)=b,a
,可得M(a,b)=b,a![]() .存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,即可得出.
.存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,即可得出.
(3)M(a,b)![]() |t﹣at2﹣b|
|t﹣at2﹣b|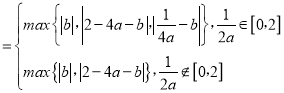 .即可得出.
.即可得出.
(1)记G(x)=2x2﹣(4x﹣1)=2(x﹣1)2﹣1,x∈[0,2].则|G(x)|的最大值为1,
且G(0)=1,G(1)=﹣1,G(2)=1.故y=4x﹣1是g(x)=2x2,x∈[0,2]的“逼近函数”.
(2)F(x)![]() (ax+b),由
(ax+b),由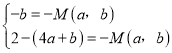 ,可得M(a,b)=b,a
,可得M(a,b)=b,a![]() .
.
存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,
即F(x)![]() x﹣b
x﹣b![]() b,故x2=1.
b,故x2=1.
由F(1)![]() b=b,可得b
b=b,可得b![]() .
.
(3)证明:M(a,b)![]() |t﹣at2﹣b
|t﹣at2﹣b
|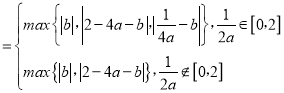 .
.
当![]() [0,2]时,2M(a,b)≥|b|+|2﹣4a﹣b|≥|2﹣4a|>1,故M(a,b)
[0,2]时,2M(a,b)≥|b|+|2﹣4a﹣b|≥|2﹣4a|>1,故M(a,b)![]() .
.

【题目】随着自媒体直播平台的迅猛发展,直播平台上涌现了许多知名三农领域创作者,通过直播或视频播放,帮助当地农民在直播平台上销售了大量的农产品,促进了农村的经济发展,当地农业与农村管理部门对近几年的某农产品年产量进行了调查,形成统计表如下:
年份 |
|
|
|
|
|
|
年份代码 |
|
|
|
|
|
|
年产量 |
|
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测![]() 年该地区该农产品的年产量;
年该地区该农产品的年产量;
(3)从![]() 年到
年到![]() 年的
年的![]() 年年产量中随机选出
年年产量中随机选出![]() 年的产量进行具体调查,求选出的
年的产量进行具体调查,求选出的![]() 年中恰有一年的产量小于
年中恰有一年的产量小于![]() 万吨的概率.
万吨的概率.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .(参考数据:
.(参考数据:![]() )
)