Question

【题目】如图，在四棱锥PABCD中，底面ABCD是矩形，点E在棱PC上异于点P，，平面ABE与棱PD交于点F

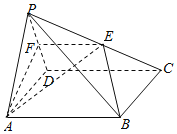
求证：；

若，求证：平面平面ABCD．

Answer 1

【答案】（1）见解析（2）见解析

【解析】

分析：（1）推导出AB∥CD，从而AB∥平面PDC，由此能证明AB∥EF．（2）结合（1）可证AB⊥AF，AB⊥平面PAD，从而得平面PAD⊥平面ABCD．

证明：（1） 因为四边形ABCD是矩形，

所以AB//CD．

又AB平面PDC，CD平面PDC，

所以AB//平面PDC，

又因为AB平面ABE，平面ABE∩平面PDC＝EF，

所以AB//EF．

（2） 因为四边形ABCD是矩形，

所以AB⊥AD．

因为AF⊥EF，（1）中已证AB//EF，

所以AB⊥AF，

又AB⊥AD，

由点E在棱PC上（异于点C），所以F点异于点D，

所以AF∩AD＝A，

AF，AD平面PAD，

所以AB⊥平面PAD，

又AB平面ABCD，

所以平面PAD⊥平面ABCD．