题目内容
抛物线 上纵坐标为
上纵坐标为 的点
的点 到焦点的距离为2.
到焦点的距离为2.
(Ⅰ)求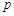 的值;
的值;
(Ⅱ)如图,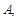

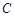 为抛物线上三点,且线段
为抛物线上三点,且线段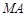 ,
, ,
,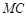 与
与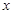 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若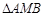 的面积是
的面积是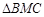 面积的
面积的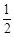 ,求直线
,求直线 的方程.
的方程.
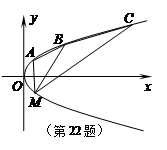
 上纵坐标为
上纵坐标为 的点
的点 到焦点的距离为2.
到焦点的距离为2.(Ⅰ)求
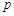 的值;
的值;(Ⅱ)如图,
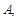

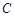 为抛物线上三点,且线段
为抛物线上三点,且线段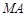 ,
, ,
,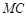 与
与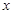 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若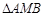 的面积是
的面积是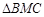 面积的
面积的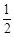 ,求直线
,求直线 的方程.
的方程.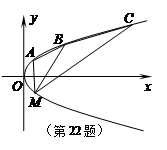
(本题15分):(Ⅰ)解:设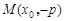 , 则
, 则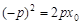 ,
,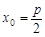 ,
,
由抛物线定义,得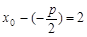 所以
所以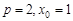 . ……5分
. ……5分
(Ⅱ)由(Ⅰ)知抛物线方程为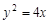 ,
,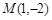 .
.
设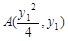 ,
,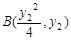 ,
,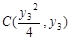 (
(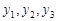 均大于零) ……6分
均大于零) ……6分
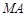 ,
, ,
,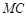 与
与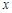 轴交点的横坐标依次为
轴交点的横坐标依次为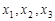 .
.
(1)当
 轴时,直线
轴时,直线 的方程为
的方程为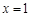 ,则
,则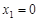 ,不合题意,舍去.
,不合题意,舍去.
……7分
(2) 与
与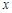 轴不垂直时,
轴不垂直时,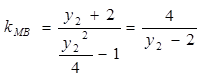 ,
,
设直线 的方程为
的方程为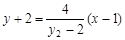 ,即
,即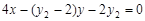 ,
,
令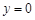 得2
得2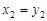 ,同理2
,同理2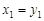 ,2
,2 , ……10分
, ……10分
因为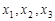 依次组成公差为1的等差数列,
依次组成公差为1的等差数列,
所以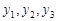 组成公差为2的等差数列. ……12分
组成公差为2的等差数列. ……12分
设点 到直线
到直线 的距离为
的距离为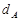 ,点
,点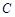 到直线
到直线 的距离为
的距离为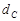 ,
,
因为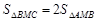 ,所以
,所以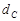 =2
=2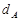 ,
,
所以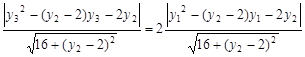 ……14分
……14分
得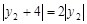 ,即
,即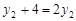 ,所以
,所以 ,
,
所以直线 的方程为:
的方程为: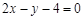 ……15分
……15分
解法二:(Ⅰ)同上. (Ⅱ)由(Ⅰ)知抛物线方程为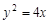 ,
,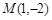 .
.
由题意,设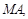
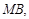
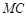 与
与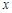 轴交点的横坐标依次为
轴交点的横坐标依次为
设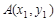 ,
,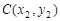 (
(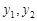 均大于零). ……6分
均大于零). ……6分
(1)当
 轴时,直线
轴时,直线 的方程为
的方程为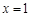 ,则
,则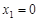 ,不合题意,舍去.
,不合题意,舍去.
……7分
(2) 与
与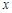 轴不垂直时,
轴不垂直时,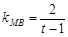
设直线 的方程为
的方程为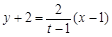 ,即
,即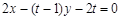 ,
,
同理直线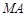 的方程为
的方程为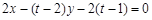 ,
,
由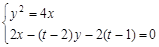 得
得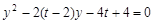
则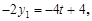 所以
所以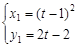 , ……12分
, ……12分
同理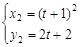 ,设点
,设点 到直线
到直线 的距离为
的距离为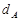 ,点
,点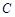 到直线
到直线 的距离为
的距离为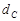 , 因为
, 因为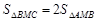 ,所以
,所以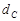 =2
=2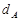 ,
,
所以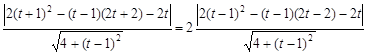 ……14分
……14分
化简得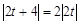 ,即
,即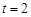 ,
,
所以直线 的方程为:
的方程为: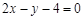 ……15分
……15分
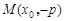 , 则
, 则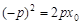 ,
,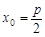 ,
,由抛物线定义,得
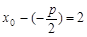 所以
所以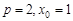 . ……5分
. ……5分(Ⅱ)由(Ⅰ)知抛物线方程为
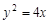 ,
,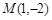 .
.设
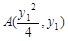 ,
,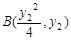 ,
,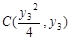 (
(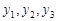 均大于零) ……6分
均大于零) ……6分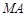 ,
, ,
,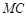 与
与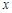 轴交点的横坐标依次为
轴交点的横坐标依次为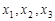 .
.(1)当

 轴时,直线
轴时,直线 的方程为
的方程为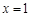 ,则
,则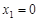 ,不合题意,舍去.
,不合题意,舍去.……7分
(2)
 与
与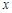 轴不垂直时,
轴不垂直时,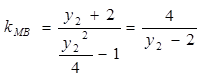 ,
,设直线
 的方程为
的方程为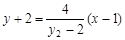 ,即
,即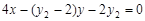 ,
,令
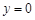 得2
得2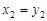 ,同理2
,同理2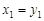 ,2
,2 , ……10分
, ……10分因为
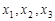 依次组成公差为1的等差数列,
依次组成公差为1的等差数列,所以
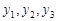 组成公差为2的等差数列. ……12分
组成公差为2的等差数列. ……12分设点
 到直线
到直线 的距离为
的距离为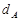 ,点
,点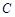 到直线
到直线 的距离为
的距离为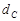 ,
,因为
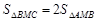 ,所以
,所以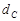 =2
=2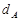 ,
,所以
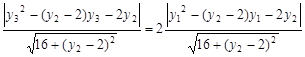 ……14分
……14分得
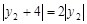 ,即
,即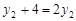 ,所以
,所以 ,
,所以直线
 的方程为:
的方程为: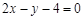 ……15分
……15分解法二:(Ⅰ)同上. (Ⅱ)由(Ⅰ)知抛物线方程为
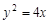 ,
,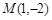 .
.由题意,设
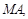
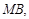
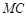 与
与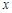 轴交点的横坐标依次为
轴交点的横坐标依次为
设
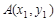 ,
,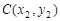 (
(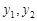 均大于零). ……6分
均大于零). ……6分(1)当

 轴时,直线
轴时,直线 的方程为
的方程为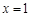 ,则
,则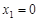 ,不合题意,舍去.
,不合题意,舍去.……7分
(2)
 与
与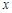 轴不垂直时,
轴不垂直时,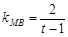
设直线
 的方程为
的方程为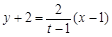 ,即
,即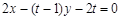 ,
,同理直线
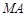 的方程为
的方程为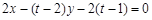 ,
,由
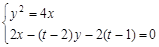 得
得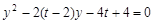
则
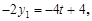 所以
所以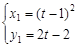 , ……12分
, ……12分同理
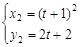 ,设点
,设点 到直线
到直线 的距离为
的距离为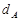 ,点
,点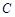 到直线
到直线 的距离为
的距离为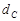 , 因为
, 因为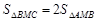 ,所以
,所以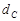 =2
=2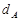 ,
,所以
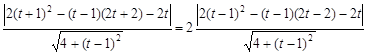 ……14分
……14分化简得
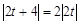 ,即
,即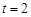 ,
,所以直线
 的方程为:
的方程为: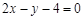 ……15分
……15分略

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
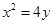 ,过定点
,过定点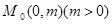 的直线
的直线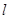 交抛物线于A、B两点.
交抛物线于A、B两点.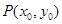 在定直线
在定直线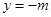 上.
上. 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线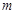 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.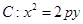 (
(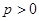 )上一点
)上一点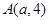 到其准线的距离为
到其准线的距离为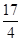 .
.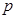 与
与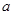 的值;
的值;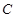 上动点
上动点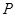 的横坐标为
的横坐标为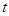 (
(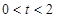 ),过点
),过点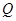 ,交
,交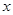 轴于
轴于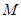 点(直线
点(直线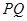 的斜率记作
的斜率记作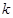 ).过点
).过点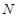 .若
.若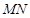 恰好是
恰好是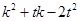 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.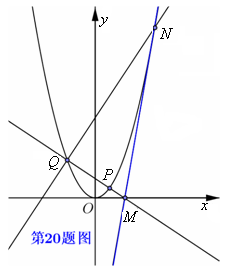
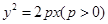 ,当过
,当过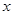 轴上一点
轴上一点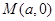 的直线
的直线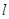 与抛物线交于
与抛物线交于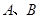 两点时,
两点时,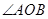 为锐角,则
为锐角,则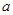 的取值范围 ( )
的取值范围 ( )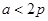
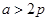
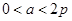
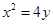 的焦点为F,A、B是热线上的两动点,且
的焦点为F,A、B是热线上的两动点,且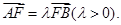 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。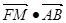 为定值;
为定值;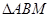 的面积为S,写出
的面积为S,写出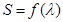 的表达式,并求S的最小值。
的表达式,并求S的最小值。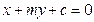 与抛物线
与抛物线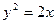 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。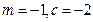 时,求证:OA⊥OB;
时,求证:OA⊥OB;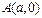 和
和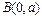 的直线与抛物线
的直线与抛物线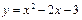 没有交点,那么实数
没有交点,那么实数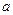 的取值范围是
的取值范围是 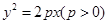 的焦点F,点
的焦点F,点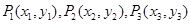 在抛物线上,且
在抛物线上,且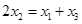 ,则有 ( )
,则有 ( )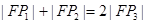
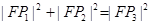
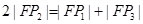
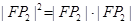
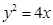 上的一个动点,则点P到点
上的一个动点,则点P到点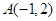 的距离与点P到
的距离与点P到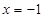 的距离之和的最小值为 .
的距离之和的最小值为 .