题目内容
(本题满分14分)
如图所示,已知曲线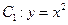 与曲线
与曲线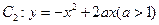 交于点O、A,直线
交于点O、A,直线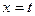 (0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
(0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。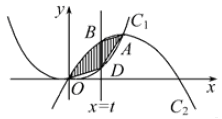
(1)写出曲边四边形ABOD(阴影部分)的面积S与t的函数关系式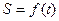 ;
;
(2)求函数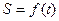 在区间
在区间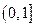 上的最大值。
上的最大值。
解:(1)由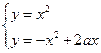
解得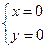 或
或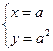 (2分)∴O(0,0),A(a,a2)。
(2分)∴O(0,0),A(a,a2)。
又由已知得B(t,-t2+2at),D(t,t2),
∴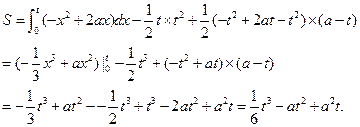
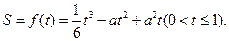 …… 6分
…… 6分
(2)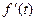 =
=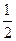 t2-2at+a2,令
t2-2at+a2,令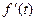 =0,即
=0,即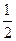 t2-2at+a2=0。解得t=(2-
t2-2at+a2=0。解得t=(2-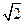 )a或t=(2+
)a或t=(2+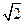 )a.
)a.
∵0<t≤1,a>1, ∴t=(2+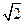 )a应舍去。 即t=(2-
)a应舍去。 即t=(2-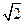 )a 8分
)a 8分
若(2-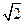 )a≥1,即a≥
)a≥1,即a≥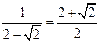 时,∵0<t≤1,∴
时,∵0<t≤1,∴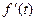 ≥0。
≥0。
∴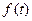 在区间
在区间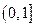 上单调递增,S的最大值是
上单调递增,S的最大值是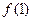 =a2-a+
=a2-a+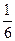 . 10分
. 10分
若(2-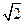 )a<1, 即1<a<
)a<1, 即1<a<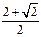 时,
时,
当0<t<(2-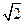 )a时,
)a时,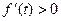 .
.
当(2-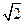 )a<t≤1时,
)a<t≤1时,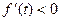 .
.
∴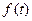 在区间(0, (2-
在区间(0, (2-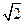 )a]上单调递增,在区间[(2-
)a]上单调递增,在区间[(2-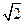 )a,1]上单调递减。
)a,1]上单调递减。
∴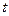 =(2-
=(2-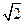 )a是极大值点,也是最大值点 12分
)a是极大值点,也是最大值点 12分
∴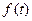 的最大值是f((2-
的最大值是f((2-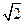 )a)=
)a)=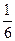 [ (2-
[ (2-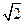 )a]3-a[(2-
)a]3-a[(2-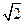 )a]2+a2(2-
)a]2+a2(2-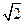 )a=
)a=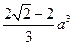 .13分
.13分
解析

练习册系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;