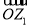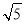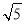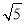题目内容
设y＝f(x)是二次函数，方程f(x)＝0有两个相等的实
根，且f′(x)＝2x＋2.
(1)求y＝f(x)的表达式；
(2)求y＝f(x)的图象与两坐标轴所围成图形的面积．
（1）f(x)＝x2＋2x＋1（2）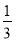
【解析】(1)设f(x)＝ax2＋bx＋c(a≠0)，则f′(x)＝2ax＋b.
又f′(x)＝2x＋2，所以a＝1，b＝2.所以f(x)＝x2＋2x＋c.
又方程f(x)＝0有两个相等实根，
即x2＋2x＋c＝0有两个相等实根，
所以Δ＝4－4c＝0，即c＝1.
故f(x)＝x2＋2x＋1.
(2)依题意，所求面积为S＝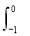
(x2＋2x＋1)dx＝
.
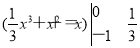练习册系列答案
相关题目
