题目内容
【题目】按照如下规则构造数表:第一行是:2;第二行是:![]() ;即3,5,第三行是:
;即3,5,第三行是:![]() 即4,6,6,8;
即4,6,6,8;![]() (即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
(即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
2
3,5
4,6,6,8
5,7,7,9,7,9,9,11
……………………………………
若第![]() 行所有的项的和为
行所有的项的和为![]() .
.
(1)求![]() ;
;
(2)试求![]() 与
与![]() 的递推关系,并据此求出数列
的递推关系,并据此求出数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]() 和
和![]() 的值.
的值.
【答案】(1)![]()
![]() (2)
(2)![]() ,
,![]() (3)
(3)![]() ,
,![]()
【解析】
(1)根据已给数据可计算![]() ,写出第5行后可计算
,写出第5行后可计算![]() ;
;
(2)根据数表的形成过程,可得递推关系:![]() ,化简后,构造新数列
,化简后,构造新数列![]() 是等差数列,通项公式可求;
是等差数列,通项公式可求;
(3)计算![]() ,并裂项得
,并裂项得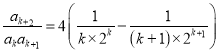 ,即用裂项相消法求得和
,即用裂项相消法求得和![]() ,然后可求得极限.
,然后可求得极限.
(1)第5行数据是6,8,8,10,8,10,10,12,8,10,10,12,10,12,12,14.
∴![]()
![]() .
.
(2)由题意,第![]() 行共有
行共有![]() 项,
项,
于是有![]()
等式两边同除![]() ,得
,得![]() ,
,
即![]() 为等差数列,公差为
为等差数列,公差为![]() ,首项为
,首项为![]()
所以![]() ,即
,即![]() .
.
(3)因为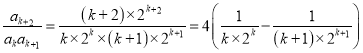
![]()
所以
所以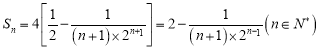 ,
,
![]() .
.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目