题目内容
命题p:“函数f(x)=-x2-ax-7在(-∞,-3)内单调递增”,命题q:“loga(a2-a+1)>0”.若p且q为假,p或q为真,则a的取值范围是( )A.[6,+∞)
B.(-∞,0]∪(6,+∞)∪{1}
C.(6,+∞)∪{0,1}
D.(6,+∞)
【答案】分析:先判断当p,q两个命题为真命题a的取值范围,根据p且q为假,p或q为真可知p,q必然一真一假,然后分p真q假,p假q真两种情况求出a的范围,再取并集即可.
解答:解:若命题p:“函数f(x)=-x2-ax-7在(-∞,-3)内单调递增”为真命题,则a≤6.
若命题q:“loga(a2-a+1)>0”为真命题,则a>0,且a≠1
∵p且q为假,p或q为真,∴p,q必然一真一假
当p真q假时,则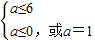 ,∴a≤0或a=1
,∴a≤0或a=1
当p假q真时,则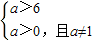 ∴a>6
∴a>6
综上,a≤0或a=1或a>6
∴a的取值范围是(-∞,0]∪(6,+∞)∪{1}
故选B
点评:本题主要考查了复合命题真假的判断,属于命题真假的应用
解答:解:若命题p:“函数f(x)=-x2-ax-7在(-∞,-3)内单调递增”为真命题,则a≤6.
若命题q:“loga(a2-a+1)>0”为真命题,则a>0,且a≠1
∵p且q为假,p或q为真,∴p,q必然一真一假
当p真q假时,则
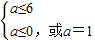 ,∴a≤0或a=1
,∴a≤0或a=1当p假q真时,则
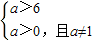 ∴a>6
∴a>6综上,a≤0或a=1或a>6
∴a的取值范围是(-∞,0]∪(6,+∞)∪{1}
故选B
点评:本题主要考查了复合命题真假的判断,属于命题真假的应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目