题目内容
19.假设在3.0秒内的任何时间,两条不相关的短信机会均等地进入同一部手机,若这两条短信进入手机的时间之差小1.0秒,手机就会受到干扰,则手机受到干扰的概率为( )| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
分析 由题意,得到所有事件集可表示为0≤x≤3,0≤y≤3.手机受则到干扰的事件发生,必有|x-y|≤1.画出平面区域,计算面积,利用几何概型的公式解答
解答 解:分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤3,0≤y≤3.由题目得,如果手机受则到干扰的事件发生,必有|x-y|≤1.三个不等式联立,则该事件即为x-y=1和y-x=1在0≤x≤3,0≤y≤3的正方形中围起来的图形:
即图中阴影区域而所有事件的集合即为正方型面积32=9,阴影部分的面积9-2×$\frac{1}{2}$(3-1)2=5,
所以阴影区域面积和正方形面积比值即为手机受到干扰的概率为$\frac{5}{9}$.
故选:C
点评 本题考查了几何概型的概率公式的应用;关键是由题意找出事件对应的不等式组,画出对应区域,然后求出面积,利用几何概型公式解答.

练习册系列答案
相关题目
4.向量$\overrightarrow a$=(2,0),$\overrightarrow b$=(x,y),若$\overrightarrow b$与$\overrightarrow b$-$\overrightarrow a$的夹角为30°,则$|{\overrightarrow b}|$的最大值为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\frac{{4\sqrt{3}}}{3}$ |
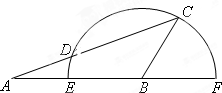 如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.
如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$. 已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为