Question

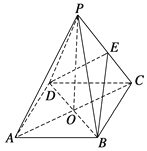
【题目】如图，在三棱锥中，，，D，E分别为BC，PD的中点，F为AB上一点，且.

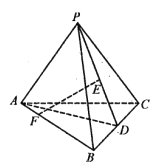
（1）求证：平面PAD；

（2）求证：平面PAC；

（3）若二面角为60°，求三棱锥的体积.

Answer 1

【答案】（1）见解析（2）见解析（3）

【解析】

（1）根据一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直，即证得；（2）根据平面外一条直线和此平面内的一条直线平行，那么这条直线和这个平面平行，在平面PAC中找一条直线与EF平行，即得证；（3）由二面角为60°，可知的面积，再由三棱锥的体积公式即得。

解：（1）证明：因为，，D是BC的中点，

所以，，

所以，平面PAD.

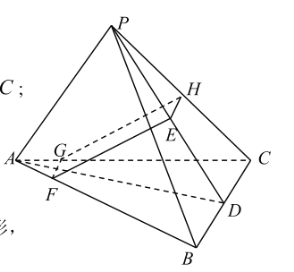
（2）证明：在AC上取一点G，使得，

取PC的中点H连接FG、GH、HE，

在中，有，，则；

在中，E、H分别是PD、PC的中点，

则，；

所以，，所以，四边形EFGH为平行四边形，

所以，，又平面PAC，平面PAC，

所以，平面PAC.

（3）由（1）知，，

所以为二面角的平面角，即，

在中，，，所以，

在中，，，所以，

所以，，

所以，三棱锥的体积.