题目内容
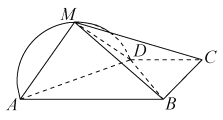
【题目】如图,点![]() 在以
在以![]() 为直径的上运动,
为直径的上运动,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若![]() ,求点
,求点![]() 平面
平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明![]() 平面
平面![]() 可得
可得![]() ,再结合
,再结合![]() 即可得出
即可得出![]() 平面
平面![]() ,故而
,故而![]() ;(2)取
;(2)取![]() 中点
中点![]() ,过
,过![]() 作
作![]() 于
于![]() ,则可证
,则可证![]() 平面
平面![]() ,从而
,从而![]() 即为所求.
即为所求.
(1)证明:∵PA⊥平面ABC,BC平面ABC,
∴PA⊥BC,
∵AB是圆的直径,∴BC⊥AC,
又AC∩PA=A,
∴BC⊥平面PAC,
又PC平面PAC.
∴BC⊥PC,
∵DE是△PBC的中位线,∴DE∥BC,
∴PC⊥DE,
∵PA=AC,D是PC的中点,
∴AD⊥PC,
又AD∩DE=D,
∴PC⊥平面ADE,又AE平面ADE,
∴PC⊥AE.
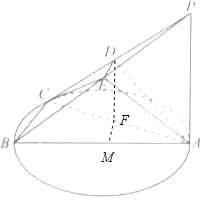
(2)解:取AC中点F,过F作FM⊥AB于M,
∵D,F分别是PC,AC的中点,
∴DF∥PA,又DF平面PAB,PA平面PAB,
∴DF∥平面PAB,
∴D到平面PAB的距离等于F到平面PAB的距离.
∵PA⊥平面ABC,FM平面ABC,
∴FM⊥PA,又FM⊥AB,PA∩AB=A,
∴FM⊥平面PAB,
∴F到平面PAB的距离为线段FM的长.
在Rt△ABC中,∵AB=2AC=2,∴AC=![]() ,
,
∴C到AB的距离为![]() =
=![]() ,
,
又F为AC的中点,∴FM=![]() .
.
∴点D到平面PAB的距离为![]() .
.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目