题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,判断并说明函数
时,判断并说明函数![]() 的零点个数.若函数
的零点个数.若函数![]() 所有零点均在区间
所有零点均在区间![]()
![]() 内,求
内,求![]() 的最小值.
的最小值.
【答案】(1)分类讨论,详见解析;(2)![]() 存在两个零点
存在两个零点![]() ,且
,且![]() ,
,![]() ;
;![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)对函数进行求导,根据![]() 的不同取值进行分类讨论,根据导函数的正负性,求出函数的单调性即可;
的不同取值进行分类讨论,根据导函数的正负性,求出函数的单调性即可;
(2)根据![]() ,结合
,结合![]() 的导数
的导数![]() 的性质进行分类讨论求解即可.
的性质进行分类讨论求解即可.
(1)![]() 的定义域为
的定义域为![]()
![]()
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时,令
时,令![]() ,
,
得![]() ,
,![]() (舍)
(舍)
当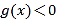 时,
时,![]() ,
,
当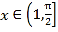 时,
时,![]()
所以![]() 在
在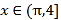 上单调递增,
上单调递增,
在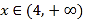 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时,
时,![]() 在
在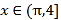 上单调递增,
上单调递增,
在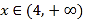 上单调递减.
上单调递减.
(2)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 单调递增,
单调递增,
![]() ,
,![]()
则![]() ,故不存在零点:
,故不存在零点:
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
所以![]()
所以![]() ,
,![]() 单调递增,
单调递增,
又![]()
![]()
所以存在唯一![]() ,使得
,使得![]()
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 单调递减,
单调递减,
![]() ,
,![]()
所以![]() ,存在使得
,存在使得![]()
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减, .
单调递减, .
又![]() ,
,![]()
因此,![]() 在
在![]() 上恒成立,
上恒成立,
故不存在零点.
当![]() 时,
时,![]() ,
,
所以![]() 单调递减,
单调递减,
因为![]() ,
,
所以![]() 单调递减,
单调递减,
又![]() ,
,
所以存在唯一![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,
故不存在零点.
综上,![]() 存在两个零点
存在两个零点![]() ,且
,且![]() ,
,![]()
因此![]() 的最小值为
的最小值为![]() .
.

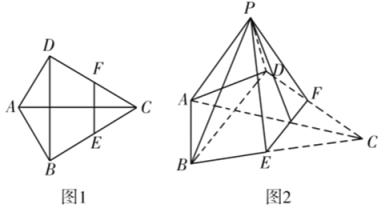
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
甲套设备的样本的频率分布直方图
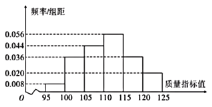
乙套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 6 | 19 | 18 | 5 | 1 |
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: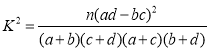 ,其中
,其中![]()
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)作与![]() 平行的直线
平行的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若
,若![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
【题目】移动支付(支付宝支付,微信支付等)开创了新的支付方式,使电子货币开始普及,为了了解习惯使用移动支付方式是否与年龄有关,对某地200人进行了问卷调查,得到数据如下:60岁以上的人群中,习惯使用移动支付的人数为30人;60岁及以下的人群中,不习惯使用移动支付的人数为40人.已知在全部200人中,随机抽取一人,抽到习惯使用移动支付的人的概率为0.6.
(1)完成如下的列联表,并判断是否有![]() 的把握认为习惯使用移动支付与年龄有关,并说明理由.
的把握认为习惯使用移动支付与年龄有关,并说明理由.
习惯使用移动支付 | 不习惯使用移动支付 | 合计(人数) | |
60岁以上 | |||
60岁及以下 | |||
合计(人数) | 200 |
(2)在习惯使用移动支付的60岁以上的人群中,每月移动支付的金额如下表:
每月支付金额 |
|
| 300以上 |
人数 | 15 |
| 5 |
现采用分层抽样的方法从中抽取6人,再从这6人中随机抽取2人,求这2人中有1人月支付金额超过3000元的概率.
附: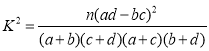 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |