题目内容
【题目】已知椭圆![]() ,焦距为2,离心率
,焦距为2,离心率![]() 为
为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
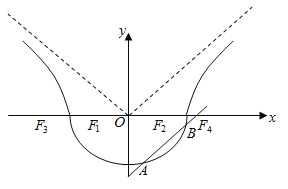
(2)过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】
(1)根据焦距和离心率求![]() ,再求
,再求![]() 即得;
即得;
(2)由题意,![]() 四点共圆,该圆的方程为
四点共圆,该圆的方程为![]() ,则直线
,则直线![]() 为圆
为圆![]() 与圆
与圆![]() 的公共弦所在的直线,求出直线
的公共弦所在的直线,求出直线![]() 的方程,求出点
的方程,求出点![]() 、点
、点![]() 的坐标. 设
的坐标. 设![]() ,则
,则![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,代入椭圆的方程,利用韦达定理、弦长公式就能求出
,代入椭圆的方程,利用韦达定理、弦长公式就能求出![]() 的面积的最大值.
的面积的最大值.
(1)由题意, ![]() ,解得
,解得![]() ,由
,由![]() ,解得
,解得![]() ;
;
所以椭圆的标准方程为![]() ;
;
(2)由题意,得![]() 四点共圆,该圆的方程为
四点共圆,该圆的方程为![]() ,
,
又圆![]() 的方程为
的方程为![]() ,两圆方程相减,得直线
,两圆方程相减,得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
设![]() ,则
,则![]() ,因此
,因此![]() 最大,
最大, ![]() 就最大,
就最大,
由题意直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]() ,
,
由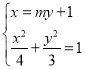 得
得![]() ,
,
所以![]() ,
,
又直线![]() 与椭圆
与椭圆![]() 交于不同的两点,则
交于不同的两点,则![]() ,即
,即![]() ,
,
![]() ,
,
令![]() ,则
,则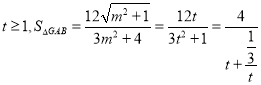 ,
,
令 ,则函数
,则函数![]() 在
在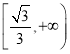 上单调递增,
上单调递增,
即当![]() 时,
时, ![]() 在
在![]() 上单调递增,因此有
上单调递增,因此有![]() ;
;
所以![]() ,当
,当![]() 时取等号.
时取等号.
故![]() 面积的最大值为3
面积的最大值为3

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;