题目内容
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)作与![]() 平行的直线
平行的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若
,若![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据点![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() ,直线与椭圆方程联立,解得点
,直线与椭圆方程联立,解得点![]() 的坐标
的坐标![]() ,则有
,则有![]() ,再由
,再由![]() 求解.
求解.
(2)设直线![]() 的方程为
的方程为![]()
![]() .由
.由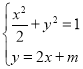 可得
可得![]() ,由韦达定理
,由韦达定理![]() ,求得点M的横纵坐标
,求得点M的横纵坐标![]() ,
,![]() ,建立模型
,建立模型![]()
![]()
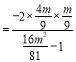
![]() ,由
,由![]() ,得到
,得到![]() ,或
,或![]() .然后用函数法求范围.
.然后用函数法求范围.
(1)由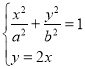 可得
可得![]() ,
,![]() .
.
根据对称性,不妨设点![]() 在第一象限,则点
在第一象限,则点![]() 的坐标为
的坐标为![]() ,
,
设椭圆的焦距为2c,由条件可得![]() ,
,
即![]() ,
,
由椭圆的离心率可得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]()
![]() ,解得
,解得![]() ,故
,故![]() .
.
故椭圆![]() 的方程为
的方程为![]()
(2)设直线![]() 的方程为
的方程为![]()
![]() .
.
由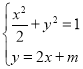 可得
可得![]() ,
,
![]() ,即
,即![]() ,
,
所以,![]() ,或
,或![]() .
.
设![]() ,
,
则![]() .
.
则![]() ,
,![]() .
.
则![]() ,
,
![]()
![]()
![]()
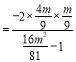
![]() .
.
当![]() 时,
时,![]() ,且
,且![]() 在
在![]() 和
和![]() 上的取值范围相同,
上的取值范围相同,
故只需求![]() 在
在![]() 上的取值范围.
上的取值范围.
而![]() 在
在![]() 和
和![]() 上随
上随![]() 的增大而增大.
的增大而增大.
![]()
![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目