题目内容
【题目】有10名选手![]() ,他们的积分分别为9,8,7,6,5,4,3,2,1,0,名次分别为第1,2,3,4,5,6,7,8,9,10.现进行单循环比赛(即任意两名选手之间都恰进行一场比赛),且每场比赛都要分出胜负.若名次靠前的选手胜了名次靠后的选手,则胜者得1分,负者得0分;若名次靠后的选手胜了名次靠前的选手,则胜者得2分,负者得0分.全部比赛结束后计算每名选手的累计积分(即这次单循环所得的分数与之前的积分相加所得的和),并根据累计积分进行重新排名,求新的冠军累计积分的最小值(允许名次并列).
,他们的积分分别为9,8,7,6,5,4,3,2,1,0,名次分别为第1,2,3,4,5,6,7,8,9,10.现进行单循环比赛(即任意两名选手之间都恰进行一场比赛),且每场比赛都要分出胜负.若名次靠前的选手胜了名次靠后的选手,则胜者得1分,负者得0分;若名次靠后的选手胜了名次靠前的选手,则胜者得2分,负者得0分.全部比赛结束后计算每名选手的累计积分(即这次单循环所得的分数与之前的积分相加所得的和),并根据累计积分进行重新排名,求新的冠军累计积分的最小值(允许名次并列).
【答案】12
【解析】
新的冠军累计积分的最小值为12.
若新的冠军的得分不超过11分,则
![]() 最多胜2场;
最多胜2场;![]() 最多胜3场;
最多胜3场;![]() 最多胜4场;
最多胜4场;![]() 最多胜5场.
最多胜5场.
![]() 最多增加6分,但是开始时积分比他少的选手只有5人,
最多增加6分,但是开始时积分比他少的选手只有5人,
因此,若增加6分,他与名次比他靠前的选手的比赛至少胜1场,
这样,他与名次靠后的选手的比赛最多胜4场.从而,他最多胜5场.
![]() 最多增加7分,但是开始时积分比他少的选手只有4人,
最多增加7分,但是开始时积分比他少的选手只有4人,
因此,若增加7分,他与名次比他靠前的选手的比赛至少胜2场,
这样,他与名次靠后的选手的比赛最多胜3场.从而,他最多胜5场.
![]() 最多增加8分,但是开始时积分比他少的选手只有3人,
最多增加8分,但是开始时积分比他少的选手只有3人,
因此,若增加8分,他与名次比他靠前的选手的比赛至少胜3场,
这样,他与名次靠后的选手的比赛最多胜2场.从而,他最多胜5场.
![]() 最多增加9分,但是开始时积分比他少的选手只有2人,
最多增加9分,但是开始时积分比他少的选手只有2人,
因此.若增加9分,他与名次比他靠前的选手的比赛至少胜4场,
这样,他与名次靠后的选手的比赛最多胜1场.从而,他最多胜5场.
![]() 最多增加10分,但是开始时积分比他少的选手只有1人,
最多增加10分,但是开始时积分比他少的选手只有1人,
因此,若增加10分,他与名次比他靠前的选手的比赛至少胜5场.从而,他最多胜5场.
![]() 最多增加11分,他与名次比他靠前的选手的比赛最多胜5场,从而,他最多胜5场.
最多增加11分,他与名次比他靠前的选手的比赛最多胜5场,从而,他最多胜5场.
综上,所有选手胜的场数最多为![]() ,但是每两名选手进行的一场比赛都会胜一场,共胜
,但是每两名选手进行的一场比赛都会胜一场,共胜![]() 场,矛盾.
场,矛盾.
下面的例子说明新的冠军累计积分可以是12分.
![]() 胜
胜![]() ,负
,负![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,负
,负![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,负
,负![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,负
,负![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,负
,负![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,累计得分为
,累计得分为![]() ;
;
![]() 胜
胜![]() ,累计得分为
,累计得分为![]() ;
;
![]() 累计得分为
累计得分为![]() .
.

【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生7次考试的成绩.
进行分析.下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(2)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
参考公式:方差公式:![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.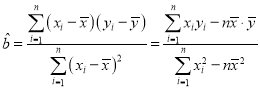 ,
,![]() 。
。