题目内容
【题目】已知函数f(x)对任意x，y∈R，总有f(x)＋f(y)＝f(x＋y)，且当x>0时，f(x)<0，f(1)＝－
.
(1)求证：f(x)是R上的单调减函数．
(2)求f(x)在[－3,3]上的最小值．
【答案】（1）详见解析（2）－2
【解析】
（1）本题中，需要证明的是函数的增减性，则需要回归定义，从定义出发，根据增减性采用合适的拼凑法来进行证明
（2）抽象函数函数值的求法需要通过合理赋值求得，需要考虑函数的增减性。
(1)证明：设x1，x2是任意的两个实数，且x1<x2，
则x2－x1>0，因为x>0时，f(x)<0，
所以f(x2－x1)<0，
又因为x2＝(x2－x1)＋x1，
所以f(x2)＝f[(x2－x1)＋x1]
＝f(x2－x1)＋f(x1)，
所以f(x2)－f(x1)＝f(x2－x1)<0，
所以f(x2)<f(x1)．
所以f(x)是R上的单调减函数．
(2)由(1)可知f(x)在R上是减函数，
所以f(x)在[－3,3]上也是减函数，
所以f(x)在[－3,3]上的最小值为f(3)．
而f(3)＝f(1)＋f(2)＝3f(1)＝3×
＝－2.
所以函数f(x)在[－3,3]上的最小值是－2.
阅读快车系列答案【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在
内，发布成绩使用等级制，各等级划分标准见下表．
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定：A，B，C三级为合格等级，D为不合格等级为了解该校高三年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．
按照
，
，
，
，
的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示
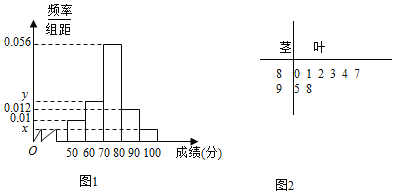
求n和频率分布直方图中的x，y的值，并估计该校高一年级学生成绩是合格等级的概率；
根据频率分布直方图，求成绩的中位数
精确到
；
在选取的样本中，从A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是A等级的概率．
【题目】（本小题满分12分）某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
（1）从统计数据看，甲、乙两个班哪个班成绩更稳定（用数字特征说明）；
（2）在本次训练中，从两班中分别任选一个同学，比较两人的投中次数，求甲班同学投中次数高于乙班同学投中次数的概率．
