Question

设动点的坐标为（x、），且动点到定点，的距离之和为8.

   （I）求动点的轨迹的方程；

   （Ⅱ）过点作直线与曲线交于、两点，若（为坐标原点），是否存在直线，使得四边形为矩形，若存在,求出直线的方程，若不存在，请说明理由.

Answer 1

解：（I）由已知可得，动点的轨迹是到定点，的距离之和为8的椭圆.

      则曲线的方程是.   

   （Ⅱ）因为直线过点，若直线的斜率不存在，则的方程为，与椭圆的两个交点、为椭圆的顶点.

       由，则与重合，与为四边形矛盾.

       若直线的斜率存在，设方程为，，.

       由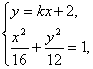得.

       恒成立.

       由根与系数关系得：，.

       因为，所以四边形为平行四边形.

       若存在直线使四边形为矩形，则.

       所以.

       所以.

       即.

       化简得： . 与斜率存在矛盾.

       则不存在直线，使得四边形为矩形.