题目内容
设函数f(α)=sinα+
cosα,其中,角α的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤α≤π.
(1)若P点的坐标为(
,1),求f(α)的值;
(2)若点P(x,y)为平面区域
上的一个动点,试确定角α的取值范围,并求函数f(α)的最小值和最大值.
| 3 |
(1)若P点的坐标为(
| 3 |
(2)若点P(x,y)为平面区域
|
分析:(1)由三角函数的定义,算出sinα=
,cosα=
,代入即可得到求f(α)的值;
(2)作出题中不等式组表示的平面区域,得到如图所示的△ABC及其内部区域,运动点P并加以观察,可得α∈[
,
].利用辅助角公式化简得f(α)=2sin(α+
),由α+
∈[
,
]结合正弦函数的图象与性质加以计算,可得函数f(α)的最小值和最大值.
| 1 |
| 2 |
| ||
| 2 |
(2)作出题中不等式组表示的平面区域,得到如图所示的△ABC及其内部区域,运动点P并加以观察,可得α∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
解答:解:(1)∵P点的坐标为(
,1),可得r=|OP|=
=2,
∴由三角函数的定义,得sinα=
,cosα=
,
故f(α)=sinα+
cosα=
+
×
=2.
(2)作出不等式组
表示的平面区域,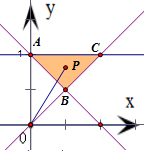
得到如图所示的△ABC及其内部区域,
其中A(0,1)、B(0.5,0.5),C(1,1),
∵P为区域内一个动点,且P为角α终边上的一点,
∴运动点P,可得当P与A点重合时,α=
达到最大值;
当P与线段BC上一点重合时,α=
达到最小值.由此可得α∈[
,
].
∵f(α)=sinα+
cosα=2sin(α+
),
∴由α∈[
,
],可得α+
∈[
,
],
当α+
=
即α=
时,f(α)有最小值2sin
=1;
当α+
=
即α=
时,f(α)有最大值2sin
=
.
综上所述函数f(α)的最小值为1,最大值为
.
| 3 |
| 3+1 |
∴由三角函数的定义,得sinα=
| 1 |
| 2 |
| ||
| 2 |
故f(α)=sinα+
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(2)作出不等式组
|

得到如图所示的△ABC及其内部区域,
其中A(0,1)、B(0.5,0.5),C(1,1),
∵P为区域内一个动点,且P为角α终边上的一点,
∴运动点P,可得当P与A点重合时,α=
| π |
| 2 |
当P与线段BC上一点重合时,α=
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∵f(α)=sinα+
| 3 |
| π |
| 3 |
∴由α∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
当α+
| π |
| 3 |
| 5π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
当α+
| π |
| 3 |
| 7π |
| 12 |
| π |
| 4 |
| 7π |
| 12 |
| ||||
| 2 |
综上所述函数f(α)的最小值为1,最大值为
| ||||
| 2 |
点评:本题给出角α终边上的一点P,在P满足特殊条件下求f(α)=sinα+
cosα的最值.着重考查了任意角三角函数的定义、二元一次不等式组表示的平面区域和三角函数的图象与性质等知识,属于中档题.
| 3 |

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 )+sin(wx-
)+sin(wx- )上单调递增 B.f(x)在(0,
)上单调递增 B.f(x)在(0,  )上单调递增 D.f(x)在(0,
)上单调递增 D.f(x)在(0,