题目内容
设函数f(α)=sinα+
cosα,其中,角α的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤α≤π
(I)若P点的坐标为(-
,1),求f(α)的值;
(II)若点P(x,y)为平面区域
上的一个动点,试确定角α的取值范围,并求函数f(α)的值域.
| 3 |
(I)若P点的坐标为(-
| 3 |
(II)若点P(x,y)为平面区域
|
分析:(I)由三角函数的定义,算出sinα、cosα的值,即可求出f(α)的值;
(II)作出题中不等式组表示的平面区域,将点P在区域内运动可得α∈[
,
].根据辅助角公式,化简得f(α)=2sin(α+
),再利用正弦函数的图象与性质加以计算,即可得到函数f(α)的值域.
(II)作出题中不等式组表示的平面区域,将点P在区域内运动可得α∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
解答: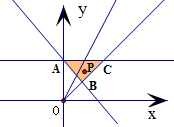 解:(I)∵P点的坐标为(-
解:(I)∵P点的坐标为(-
,1),
∴|OP|=
=2,得sinα=
,cosα=
=-
因此,f(α)=sinα+
cosα=
+
•(-
)=-1;
(II)作出不等式
表示的平面区域,
得到如图所示的△ABC及其内部.
其中A(0,1),B(
,
),C(1,1).
∵点P(x,y)为平面区域内的一个动点,∴α∈[
,
].
f(α)=sinα+
cosα=2sin(α+
),
∵α+
∈[
,
],
∴当α=
时,f(α)=2sin
=
达到最大值;当α=
时,f(α)=2sin
=1达到最小值.
由此可得函数f(α)的值域为[1,
].
 解:(I)∵P点的坐标为(-
解:(I)∵P点的坐标为(-| 3 |
∴|OP|=
| 3+1 |
| 1 |
| 2 |
-
| ||
| 2 |
| ||
| 2 |
因此,f(α)=sinα+
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(II)作出不等式
|
得到如图所示的△ABC及其内部.
其中A(0,1),B(
| 1 |
| 2 |
| 1 |
| 2 |
∵点P(x,y)为平面区域内的一个动点,∴α∈[
| π |
| 4 |
| π |
| 2 |
f(α)=sinα+
| 3 |
| π |
| 3 |
∵α+
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
∴当α=
| π |
| 4 |
| 7π |
| 12 |
| ||||
| 2 |
| π |
| 2 |
| 5π |
| 6 |
由此可得函数f(α)的值域为[1,
| ||||
| 2 |
点评:本题给出点P是角α终边上一点,求f(α)=sinα+
cosα的值域.着重考查了三角函数的定义、三角函数的图象与性质和函数值域求法等知识,属于中档题.
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)
(考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)



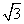 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π,
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π,  ,求f(θ)的值;
,求f(θ)的值;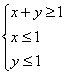 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.