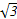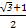题目内容
已知焦点在x轴上的椭圆的离心率为 ,且它的长轴长等于圆C:x2+y2-2x-15=0的半径,则椭圆的标准方程是( )
,且它的长轴长等于圆C:x2+y2-2x-15=0的半径,则椭圆的标准方程是( )
A.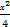 + +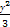 =1 =1 | B.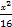 + +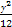 =1 =1 |
C.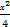 +y2=1 +y2=1 | D.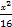 + + =1 =1 |
A
解析

练习册系列答案
相关题目
设定点M1(0,-3),M2(0,3),动点P满足条件|PM1|+|PM2|=a+ (其中a是正常数),则点P的轨迹是( )
(其中a是正常数),则点P的轨迹是( )
| A.椭圆 | B.线段 |
| C.椭圆或线段 | D.不存在 |
抛物线 上的一点M到焦点的距离为1,则点M到y轴的距离是 ( )
上的一点M到焦点的距离为1,则点M到y轴的距离是 ( )
A. | B. |
| C.1 | D. |
己知抛物线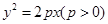 的焦点F恰好是双曲线
的焦点F恰好是双曲线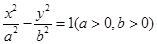 的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为( )
A. +1 +1 | B.2 | C. | D. -1 -1 |
顶点在原点,准线与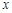 轴垂直,且经过点
轴垂直,且经过点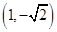 的抛物线方程是( )
的抛物线方程是( )
A.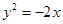 | B.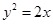 | C.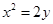 | D.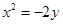 |
斜率为1的直线l与椭圆 +y2=1交于不同两点A,B,则|AB|的最大值为( )
+y2=1交于不同两点A,B,则|AB|的最大值为( )
| A.2 | B. |
C. | D. |
 ·
· 的值等于( )
的值等于( ) -y2=1的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值为( )
-y2=1的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值为( )