[题目]已知点(1.2)是函数的图象上一点.数列的前项和是.(1)求数列的通项公式,(2)若.求数列的前n项和题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知点（1，2）是函数的图象上一点，数列的前项和是.

（1）求数列的通项公式；

（2）若，求数列的前n项和

【答案】（1）an＝2n－1；（2）Tn＝(n－1)2n＋1.

【解析】

（1）由点（1,2）在图像上求出，再利用法求出。

（2）利用错位相减法求和，注意相减时项的符号，求和时项数的确定。

(1)把点(1,2)代入函数f(x)＝ax得a＝2，

所以数列{an}的前n项和为Sn＝f(n)－1＝2n－1.

当n＝1时，a1＝S1＝1；

当n≥2时，an＝Sn－Sn－1＝2n－2n－1＝2n－1，对n＝1时也适合，

∴an＝2n－1.

(2)由a＝2，bn＝logaan＋1得bn＝n，

所以anbn＝n·2n－1.

Tn＝1·20＋2·21＋3·22＋…＋n·2n－1，①

2Tn＝1·21＋2·22＋3·23＋…＋(n－1)·2n－1＋n·2n.②

由①－②得：－Tn＝20＋21＋22＋…＋2n－1－n·2n，

所以Tn＝(n－1)2n＋1.

练习册系列答案

新课标同步训练系列答案

一线名师口算应用题天天练一本全系列答案

【题目】如图，已知点，是以为底边的等腰三角形，点在直线:上．

（1）求边上的高所在直线的方程；

（2）求的面积．

【题目】已知函数，其中．

（1）当时，写出函数的单调区间；(直接写出答案，不必写出证明过程)

（2）当时，求函数的零点；

（3）当时，求函数在上的最小值．

【题目】某城市地铁项目正在紧张建设中，通车后将给市民出行带来便利.已知某条线路通车后，地铁的发车时间间隔（单位：分钟）满足.经测算，地铁载客量与发车时间间隔相关，当时地铁为满载状态，载客量为人，当时，载客量会减少，减少的人数与的平方成正比，且发车时间间隔为分钟时的载客量为人，记地铁载客量为.

（1）求的表达式，并求当发车时间间隔为分钟时，地铁的载客量；

（2）若该线路每分钟的净收益为（元），问当发车时间间隔为多少时，该线路每分钟的净收益最大？每分钟的最大净收益为多少？

【题目】某工厂为了对本工厂工人的理论成绩与实践能力进行分析，决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析．如果随机抽取的7名工人的理论成绩与实践能力值单位：分对应如下表：

工人序号i	1	2	3	4	5	6	7
理论成绩	60	65	70	75	85	87	90
实践能力值	70	77	80	85	90	86	93

（1）求这7名工人的理论成绩与实践能力值的中位数、极差；

（2）若规定85分以上包括85分为优秀，从这7名工人中抽取3名工人，记3名工人中理论成绩和实践能力值均为优秀的人数为X，求X的分布列和期望；

（3）根据下表数据，求实践能力值y关于理论成绩x的线性回归方程．系数精确到

附：线性回归方程中，，．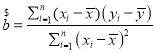


76	83	812	526

【题目】已知函数（a为常数）.

（Ⅰ）当时，求函数的单调区间；

（Ⅱ）当时，不等式恒成立，求实数的取值范围.

【题目】圆周上有个点，用弦两两连结起来，其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为.

（1）.直接画图求出，，，，；

（2）.确定的表达式.

【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学基本公式大赛，他们取得的成绩(满分100分)的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83.

（1）求x和y的值；

（2）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．

试题分类