题目内容
椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,若椭圆
,若椭圆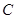 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆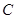 的离心率的取值范围是( )
的离心率的取值范围是( )
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,若椭圆
,若椭圆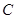 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆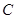 的离心率的取值范围是( )
的离心率的取值范围是( )A.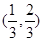 | B. | C. | D. |
D
试题分析:解:
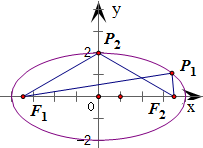
①当点P与短轴的顶点重合时,△F1F2P构成以F1F2为底边的等腰三角形,此种情况有2个满足条件的等腰△F1F2P;②当△F1F2P构成以F1F2为一腰的等腰三角形时,以F2P作为等腰三角形的底边为例,∵F1F2=F1P,∴点P在以F1为圆心,半径为焦距2c的圆上,因此,当以F1为圆心,半径为2c的圆与椭圆C有2交点时,存在2个满足条件的等腰△F1F2P,此时a-c<2c,解得a<3c,所以离心率e>
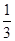 当e=
当e=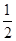 时,△F1F2P是等边三角形,与①中的三角形重复,故e≠
时,△F1F2P是等边三角形,与①中的三角形重复,故e≠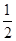 同理,当F1P为等腰三角形的底边时,在e>
同理,当F1P为等腰三角形的底边时,在e>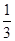 且e≠
且e≠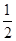 时也存在2个满足条件的等腰△F1F2P,这样,总共有6个不同的点P使得△F1F2P为等腰三角形,综上所述,离心率的取值范围是:e∈
时也存在2个满足条件的等腰△F1F2P,这样,总共有6个不同的点P使得△F1F2P为等腰三角形,综上所述,离心率的取值范围是:e∈ ,故选D.
,故选D.点评:本题给出椭圆的焦点三角形中,共有6个不同点P使得△F1F2P为等腰三角形,求椭圆离心率e的取值范围.着重考查了椭圆的标准方程和简单几何性质等知识,属于基础题

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 的离心率为
的离心率为 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为 ,直线
,直线 交椭圆于不同的两点
交椭圆于不同的两点 。
。 到直线
到直线 的距离为
的距离为 ,求
,求 面积的最大值。
面积的最大值。 是双曲线
是双曲线 的两个顶点,点
的两个顶点,点 是双曲线上异于
是双曲线上异于 (
( 为坐标原点)交椭圆
为坐标原点)交椭圆 于点
于点 ,如果设直线
,如果设直线 的斜率分别为
的斜率分别为 ,且
,且 ,假设
,假设 ,则
,则 的值为( )
的值为( )
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,P是C上的点,
,P是C上的点, ⊥
⊥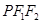 =
= ,则C的离心率为( )
,则C的离心率为( )



 :
:
 过点
过点 ,上、下焦点分别为
,上、下焦点分别为 、
、 ,
, .直线
.直线 与椭圆交于
与椭圆交于 两点,线段
两点,线段 中点为
中点为 .
. ,若曲线
,若曲线 与区域
与区域 的最小值.
的最小值.
 是椭圆
是椭圆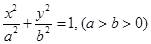 的左焦点,直线
的左焦点,直线 方程为
方程为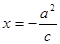 ,直线
,直线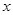 轴交于
轴交于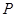 点,
点,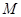 、
、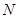 分别为椭圆的左右顶点,已知
分别为椭圆的左右顶点,已知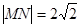 ,且
,且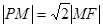 .
.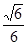 的直线交椭圆于
的直线交椭圆于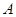 、
、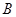 两点,求三角形
两点,求三角形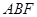 面积.
面积. 过点
过点 ,且离心率
,且离心率 .
. 的标准方程;
的标准方程; 的直线
的直线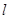 交椭圆于不同的两点M、N,且满足
交椭圆于不同的两点M、N,且满足 (其中点O为坐标原点),若存在,求出直线
(其中点O为坐标原点),若存在,求出直线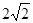 ,0)和F2(
,0)和F2(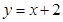 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。