题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 为坐标原点,若椭圆
为坐标原点,若椭圆![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() (
(![]() 下
下![]() 上),且
上),且![]() 两点满足
两点满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 上异于其顶点的任一点
上异于其顶点的任一点![]() ,作
,作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,且直线
,且直线![]() 在
在![]() 轴、
轴、![]() 轴上的截距分别为
轴上的截距分别为![]() ,证明:
,证明:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)设![]() ,然后根据向量数量积求得
,然后根据向量数量积求得![]() 的值,再结合离心率求得
的值,再结合离心率求得![]() 的值,由此求得椭圆方程;(2).设点
的值,由此求得椭圆方程;(2).设点![]() ,然后根据条件求得
,然后根据条件求得![]() 的方程,从而求得直线
的方程,从而求得直线![]() 在
在![]() 轴、
轴、![]() 轴上的截距为
轴上的截距为![]() ,进而使问题得证.
,进而使问题得证.
试题解析:(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,设
,设![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,∴
,∴![]() ,①
,①
又椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,②
,②
又![]() ,③
,③
由①②③,解得![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() ................................... 6分
................................... 6分
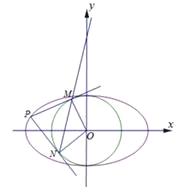
(2)如图,设点![]() ,由
,由![]() 是
是![]() 的切点知,
的切点知,![]() ,
,
所以![]() 四点在同一圆上,且圆的直径为
四点在同一圆上,且圆的直径为![]() ,
,
则圆心为![]() ,其方程为
,其方程为![]() ,
,
即![]() ,④
,④
即点![]() 满足话中④,又点
满足话中④,又点![]() 都在
都在![]() 上,
上,
所以![]() 坐标也满足方程
坐标也满足方程![]() ,⑤
,⑤
⑤-④得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,所以
,所以![]() ,
,
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,即
,即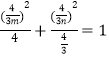 中,
中,
即![]() ,即
,即![]() 为定值.........................12分
为定值.........................12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
