题目内容
【题目】徐州、苏州两地相距500千米，一辆货车从徐州匀速行驶到苏州，规定速度不得超过100千米/小时．已知货车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为0.01；固定部分为a元（a＞0）．
（1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定义域；
（2）为了使全程运输成本最小，汽车应以多大速度行驶？
【答案】解：（1）依题意知汽车从甲地匀速行驶到乙地所用时间为
，全程运输成本为y=a×+0.01v2×=
+5v
故所求函数及其定义域为y=+5v，v∈（0，100]
（2）依题意知a，v都为正数，故有+5v
，当且仅当=5v，即v=10
时，等号成立
①若10≤100，即0＜a≤100时，则当v=10时，全程运输成本y最小．
②若10＞100，即a＞100时，则当v∈（0，100]时，有y′=﹣
+5=
．
∴函数在v∈（0，100]上单调递减，也即当v=100时，全程运输成本y最小．
综上知，为使全程运输成本y最小，当0＜a≤100时行驶速度应为v=10千米/时；当a＞100时行驶速度应为v=100千米/时．
【解析】（1）求出汽车从甲地匀速行驶到乙地所用时间，根据货车每小时的运输成本（以元为单位）由可变部分和固定部分组成，即可得到全程运输成本，以及函数的定义域；
（2）利用基本不等式可得+5v ， 当且仅当=5v，即v=10时，等号成立，再进行分类讨论即可得出结论．
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响，某市环保监测站2014年10月连续10天（从左到右对应1号至10号）采集该市某地平均风速及空气中氧化物的日均浓度数据，制成散点图如图所示．
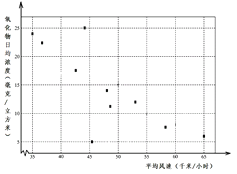
（Ⅰ）同学甲从这10天中随机抽取连续5天的一组数据，计算回归直线方程．试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率；
（Ⅱ）现有30名学生，每人任取5天数据，对应计算出30个不同的回归直线方程．已知30组数据中有包含氧化物日均浓度最值的有14组．现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测，若预测值与实测值差的绝对值小于2，则称之为“拟合效果好”，否则为“拟合效果不好”．根据以上信息完成下列2×2联表，并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关．
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
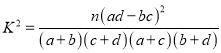（其中
）.
