题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)设函数![]() ,若存在
,若存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)实数
;(2)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题分析:(1)首先确定函数的定义域,进一步对![]() 求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在
求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”进一步,分别求函数
上的最大值”进一步,分别求函数![]() 和
和![]() 在区间
在区间![]() 和
和![]() 上的最大值.
上的最大值.
试题解析:(1) ![]() ,(此处若不写定义域,可适当扣分)
,(此处若不写定义域,可适当扣分)
故![]() .
.
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]()
![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(2)![]() ,则
,则![]() ,
,
而![]() ,故在
,故在![]() 上
上![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,![]()
![]()
而“存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”
上的最大值”
而![]() 在
在![]() 上的最大值为
上的最大值为![]() 中的最大者,记为
中的最大者,记为![]() .
.
所以有![]() ,
,![]() ,
,
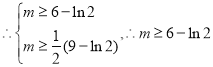 .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目