题目内容
已知函数f(x)=a0+a1x+a2x2+a3x3+…+anxn(n∈N*),且y=f(x)的图象经过点(1,n2),数列{an}为等差数列.
(1)求数列{an}的通项公式.
(2)当n为奇数时,设g(x)=![]() [f(x)-f(-x)].是否存在自然数m和M,使不等式m<g
[f(x)-f(-x)].是否存在自然数m和M,使不等式m<g![]() <M恒成立?若存在,求出M-m的最小值;若不存在,请说明理由.
<M恒成立?若存在,求出M-m的最小值;若不存在,请说明理由.
答案:
解析:
提示:
解析:
|
(1)据题意,f(1)=n2,即a0+a1+a2+…+an=n2. 令n=1,得a0+a1=1,a1=1-a0; 令n=2,得a0+a1+a2=22,a2=4-(a0+a1)=4-1=3: 令n=3,得a0+a1+a2+a3=32,a3=9-(a0+a1+a2)=9-4=5; 因为{an}为等差数列,所以d=a3-a2=5-3=2.a1=3-2=1,a0=0,an=1+(n-1)·2=2n-1.
|
提示:
|
错位相减是一种常用的特殊数列的求和方法. |

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
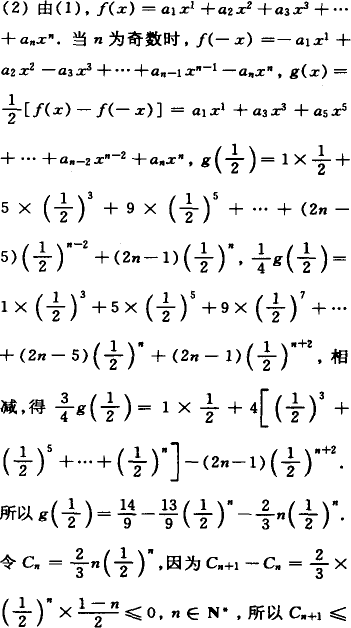

 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4. .
. (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值. )
)