题目内容
12.设E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点P为E上一动点,∠F1PF2=2θ.(1)证明:当点P为短轴端点时∠F1PF2取最大值.
(2)若∠F1PF2=90°,求∠F1PF2的面积;
(3)求证:△F1PF2的面积S=b2tanθ.
分析 (1)通过题意易知F1F2=2c,其中c2=a2-b2,设PF1=m,PF2=n,则m+n=2a,利用余弦定理计算可知1+cos∠F1PF2=$\frac{4{b}^{2}}{\frac{1}{2}(2\sqrt{m}•\sqrt{n})^{2}}$,利用基本不等式即得结论;
(2)通过设PF1=m,PF2=n,则m+n=2a,通过∠F1PF2=90°,利用勾股定理及完全平方公式化简可知mn=2b2,进而利用${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$•mn•sin∠F1PF2计算即得结论;
(3)通过(1)可知1+cos∠F1PF2=$\frac{4{b}^{2}}{2mn}$,利用二倍角公式及平方关系可知cos2θ=$\frac{{b}^{2}}{mn}$,从而mn=$\frac{{b}^{2}}{co{s}^{2}θ}$,利用${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}•mn•sin2θ$计算即得结论.
解答 (1)证明:依题意,F1F2=2c,其中c2=a2-b2,
设PF1=m,PF2=n,则m+n=2a,
由余弦定理可知m2+n2-2mncos∠F1PF2=4c2,
∴(m+n)2-2mn(1+cos∠F1PF2)=4c2,
∴1+cos∠F1PF2=$\frac{(m+n)^{2}-4{c}^{2}}{2mn}$
=$\frac{4{a}^{2}-4{c}^{2}}{2mn}$
=$\frac{4{b}^{2}}{2mn}$
=$\frac{4{b}^{2}}{\frac{1}{2}(2\sqrt{m}•\sqrt{n})^{2}}$
≥$\frac{4{b}^{2}}{\frac{1}{2}•(m+n)^{2}}$(当且仅当m=n时取等号)
=$\frac{4{b}^{2}}{\frac{1}{2}•4{a}^{2}}$
=$\frac{2{b}^{2}}{{a}^{2}}$,
即当点P为短轴端点时∠F1PF2取最大值;
(2)解:设PF1=m,PF2=n,则m+n=2a,
又∵∠F1PF2=90°,
∴m2+n2=4c2,
∴(m+n)2-2mn=4c2,
∴mn=$\frac{1}{2}$(4a2-4c2)=2b2,
∴${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$•mn•sin∠F1PF2
=$\frac{1}{2}•$2b2•sin90°
=b2;
(3)证明:依题意,F1F2=2c,其中c2=a2-b2,
设PF1=m,PF2=n,则m+n=2a,
由余弦定理可知m2+n2-2mncos∠F1PF2=4c2,
∴(m+n)2-2mn(1+cos∠F1PF2)=4c2,
∴1+cos∠F1PF2=$\frac{(m+n)^{2}-4{c}^{2}}{2mn}$
=$\frac{4{a}^{2}-4{c}^{2}}{2mn}$
=$\frac{4{b}^{2}}{2mn}$,
∴1+cos2θ=1+cos2θ-sin2θ=2cos2θ=$\frac{4{b}^{2}}{2mn}$,
∴cos2θ=$\frac{{b}^{2}}{mn}$,
∴mn=$\frac{{b}^{2}}{co{s}^{2}θ}$,
∴${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}•mn•sin2θ$
=mn•sinθcosθ
=$\frac{{b}^{2}}{co{s}^{2}θ}$•sinθcosθ
=b2tanθ.
点评 本题考查椭圆的简单性质,涉及勾股定理、余弦定理等基础知识,考查运算求解能力,注意解题方法的积累,属于中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案 如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.
如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| 对iPhone6的态度 | 计划购买的女员工 | 不计划购买的女员工 | 计划购买的男员工 | 不计划购买的男员工 |
| 频数 | 200 | 600 | 400 | 800 |
(2)若从计划购买的员工中按照性别分层抽样的方法抽取6人进行座谈,再从这6人中随机选取2人分别赠送苹果公司最新产品各一台,记获得赠品的女员工人数为X,试求X的分布列及期望.
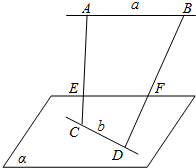 如图所示,a,b是异面直线,A,B∈a,C,D∈b,E,F分别为线段AC,BD的中点,判断直线EF和a的位置关系,并证明你的结论.
如图所示,a,b是异面直线,A,B∈a,C,D∈b,E,F分别为线段AC,BD的中点,判断直线EF和a的位置关系,并证明你的结论.