题目内容
2.设x、y满足约束条件$\left\{\begin{array}{l}x+y-5≥0\\ 2x+y-7>0\end{array}\right.$,则目标函数z=x2+y2的最小值为( )| A. | $\frac{49}{5}$ | B. | 11 | C. | $\frac{25}{2}$ | D. | 13 |
分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答 解:作出不等式组对应的平面区域如图,z的几何意义为区域内的点到原点的距离的平方,
由图象知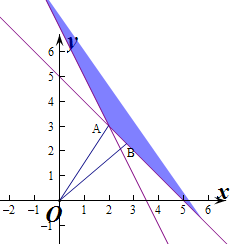
OA或OB的距离最小,
由$\left\{\begin{array}{l}{x+y-5=0}\\{2x+y-7=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即A(2,3),
则|OA|=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
圆心到直线x+y-5=0的距离d=$\frac{|-5|}{\sqrt{2}}=\frac{5}{\sqrt{2}}$,
则d<|OA|,
故z的最小值为d2=$\frac{25}{2}$,
故选:C
点评 本题主要考查线性规划的应用以及两点间的距离公式的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
14.已知i是虚数单位,则${({\frac{1-i}{1+i}})^3}$=( )
| A. | 1 | B. | i | C. | -i | D. | -1 |
 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的图象与坐标轴的三个交点为P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR=$\frac{π}{4}$,M为QR的中点,|PM|=$\sqrt{5}$.
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的图象与坐标轴的三个交点为P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR=$\frac{π}{4}$,M为QR的中点,|PM|=$\sqrt{5}$.