题目内容
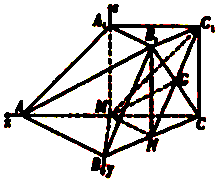
【题目】如图，在三棱台ABC﹣A1B1C1中，CC1⊥平面ABC，AB=2A1B1=2CC1 ， M，N分别为AC，BC的中点． 
（1）求证：AB1∥平面C1MN；
（2）若AB⊥BC且AB=BC，求二面角C﹣MC1﹣N的大小．
【答案】
（1）证明：连接B1N，B1C，
设B1C与NC1交于点G，在三棱台ABC﹣A1B1C1中，
AB=2A1B1，则BC=2B1C1，
而N是BC的中点，B1C1∥BC，
则B1C1 
NC，所以四边形B1C1CN是平行四边形，G是B1C的中点，
在△AB1C中，M是AC的中点，则MG∥AB1，
又AB1平面C1MN，MG平面C1MN，
所以AB1∥平面C1MN
（2）解：由CC1⊥平面ABC，可得A1M⊥平面ABC，
而AB⊥BC，AB=BC，则MB⊥AC，
所以MA，MB，MA1两两垂直，
故以点M为坐标原点，MA，MB，MA1所在的直线分别为x，y，z轴建立如图所示的空间直角坐标系．
设AB=2，则A1B1=CC1=1，AC=2 
，AM= ，
B（0， ，0），C（﹣ ，0，0），C1（﹣ ，0，1），N（﹣ 
， ，0），
则平面ACC1A1的一个法向量为 
=（0，1，0），
设平面C1MN的法向量为 
=（x，y，z），
则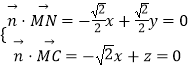 
，
取x=1，则 =（1，1， ），
cos＜ 
＞= 
，
由图形得得二面角C﹣MC1﹣N为锐角，
所以二面角C﹣MC1﹣N的大小为60°．
【解析】（1）连接B1N，B1C，设B1C与NC1交于点G，推导出四边形B1C1CN是平行四边形，从而MG∥AB1 ， 由此能证明AB1∥平面C1MN．（2）以点M为坐标原点，MA，MB，MA1所在的直线分别为x，y，z轴建立空间直角坐标系，利用向量法能求出二面角C﹣MC1﹣N的大小．
【考点精析】通过灵活运用直线与平面平行的判定，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行即可以解答此题．
