题目内容
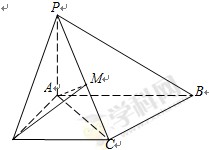
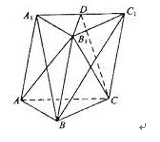
如图,在三棱柱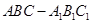 中,侧面
中,侧面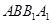 ,
,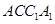 均为正方形,∠
均为正方形,∠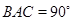 ,点
,点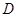 是棱
是棱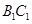 的中点.
的中点.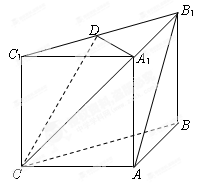
(Ⅰ)求证: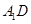 ⊥平面
⊥平面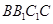 ;
;
(Ⅱ)求证: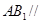 平面
平面 ;
;
(Ⅲ)求二面角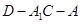 的余弦值.
的余弦值.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)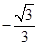 .
.
解析试题分析:(Ⅰ)由侧面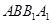 ,
,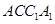 均为正方形可证明三棱柱
均为正方形可证明三棱柱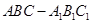 是直三棱柱. 又点
是直三棱柱. 又点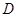 是棱
是棱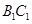 的中点可证明
的中点可证明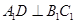 .从而通过线面垂直的判定定理可证
.从而通过线面垂直的判定定理可证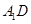 ⊥平面
⊥平面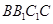 ;(Ⅱ)连结
;(Ⅱ)连结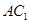 ,交
,交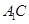 于点
于点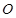 ,连结
,连结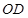 ,通过三角形中位线的知识证明线线平行,从而由线面平行的判定定理得到
,通过三角形中位线的知识证明线线平行,从而由线面平行的判定定理得到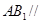 平面
平面 ;(Ⅲ)根据题中相关垂直条件构建空间直角坐标系.再找平面
;(Ⅲ)根据题中相关垂直条件构建空间直角坐标系.再找平面 的法向量及平面
的法向量及平面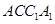 的法向量
的法向量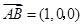 ,计算法向量的夹角,通过比较得到二面角
,计算法向量的夹角,通过比较得到二面角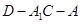 的平面角,从而得到所求.
的平面角,从而得到所求.
试题解析:(Ⅰ)证明:因为侧面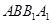 ,
,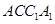 均为正方形,
均为正方形,
所以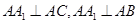 ,
,
所以 平面
平面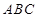 ,三棱柱
,三棱柱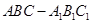 是直三棱柱. 1分
是直三棱柱. 1分
因为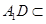 平面
平面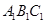 ,所以
,所以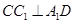 , 2分
, 2分
又因为 ,
,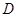 为
为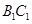 中点,
中点,
所以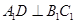 . 3分
. 3分
因为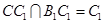 ,
,
所以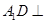 平面
平面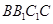 . 4分
. 4分
(Ⅱ)证明:连结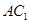 ,交
,交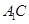 于点
于点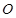 ,连结
,连结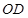 ,
,
因为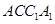 为正方形,所以
为正方形,所以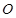 为
为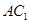 中点,
中点,
又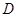 为
为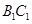 中点,所以
中点,所以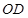 为
为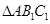 中位线,
中位线,
所以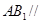
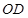 , 6分
, 6分
因为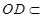 平面
平面 ,
,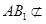 平面
平面 ,
,
所以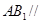 平面
平面 . 8分
. 8分
(Ⅲ)解: 因为侧面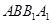 ,
,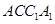 均为正方形,
均为正方形, 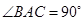 ,
,
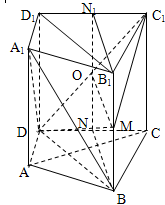
所以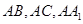 两两互相垂直,如图所示建立直角坐标系
两两互相垂直,如图所示建立直角坐标系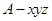 .
.
设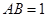 ,则
,则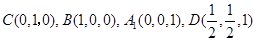 .
.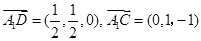 , 9分
, 9分
设平面 的法向量为
的法向量为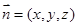 ,则有
,则有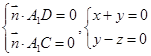
取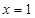 ,得
,得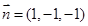 . 10分
. 10分
又因为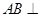 平面
平面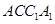 ,所以平面
,所以平面

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
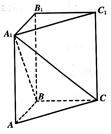
 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.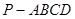 中,底面
中,底面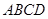 是直角梯形,
是直角梯形,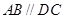 ,
,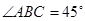 ,
,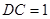 ,
,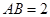 ,
,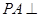 平面
平面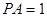 .
. 
 平面
平面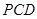 ;
; 平面
平面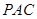 ;
; 是
是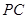 的中点,求三棱锥
的中点,求三棱锥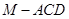 的体积.
的体积.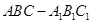 的侧面
的侧面 是菱形,
是菱形,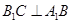
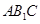
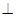 平面
平面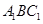 ;
;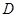 是
是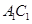 上的点,且
上的点,且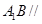 平面
平面 ,求
,求 的值.
的值.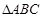 与
与 所在平面互相垂直,且
所在平面互相垂直,且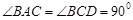 ,
,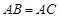 ,
,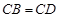 ,点
,点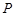 ,
, 分别在线段
分别在线段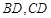 上,沿直线
上,沿直线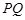 将
将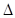
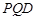 向上翻折,使
向上翻折,使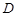 与
与 重合.
重合.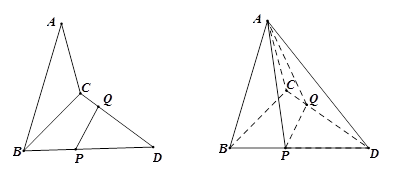
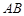
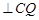 ;
; 与平面
与平面 所成的角的正弦值.
所成的角的正弦值. 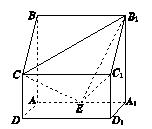
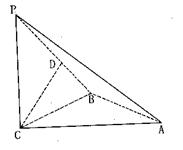
 .求线段AM的长.
.求线段AM的长.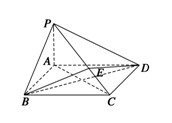
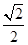 时,求四棱锥P-ABCD的外接球表面积.
时,求四棱锥P-ABCD的外接球表面积.