题目内容
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.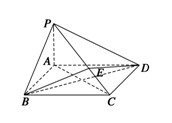
(1) 证明:BD⊥平面PAC;
(2) 若AD=2,当PC与平面ABCD所成角的正切值为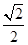 时,求四棱锥P-ABCD的外接球表面积.
时,求四棱锥P-ABCD的外接球表面积.
(1)见解析;(2)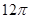 .
.
解析试题分析:(1)先利用直线与平面垂直的性质定理,得到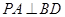 和
和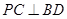 ,因为
,因为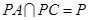 ,所以利用直线与平面垂直的判定定理可知,
,所以利用直线与平面垂直的判定定理可知,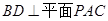 ;(2)先利用直线和平面垂直的性质定理得到
;(2)先利用直线和平面垂直的性质定理得到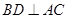 ,那么
,那么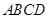 为正方形,得到边的值
为正方形,得到边的值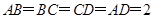 ,然后根据已知的垂直关系,找到线面角,根据线面角
,然后根据已知的垂直关系,找到线面角,根据线面角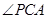 的正切值求出
的正切值求出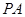 ,根据此四棱锥的性质可知,所求的外接球的直径即是线段
,根据此四棱锥的性质可知,所求的外接球的直径即是线段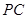 ,由已求得的量结合勾股定理求得
,由已求得的量结合勾股定理求得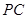 的值,再由球的表面积公式:
的值,再由球的表面积公式: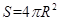 ,求此四棱锥的外接球的表面积.
,求此四棱锥的外接球的表面积.
试题解析:(1)证明 ∵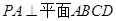 ,
,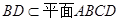 ,∴
,∴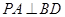 .2分
.2分
同理由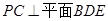 ,可证得
,可证得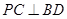 . 4分
. 4分
又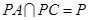 ,∴
,∴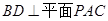 . 6分
. 6分
(2)由(1)知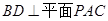 ,又
,又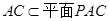 , ∴
, ∴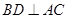 .
.
故矩形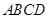 为正方形,∴
为正方形,∴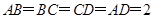 .所以
.所以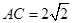 8分
8分
因为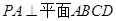 ,所以
,所以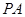 与平面
与平面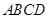 所成角为
所成角为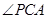 ,
,
因为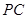 与平面
与平面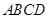 所成角的正切值为
所成角的正切值为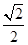 ,即
,即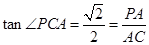 ,
,
所以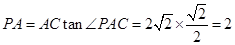 , 10分
, 10分
又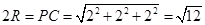 ,所以
,所以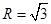 ,
,
所以四棱锥 的外接球表面积为
的外接球表面积为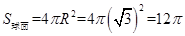 .12分
.12分
考点:1.直线与平面垂直的判定定理;2.直线与平面垂直的性质定理;3.直线和平面所成的角(线面角);4.球的体积和表面积;5.解三角形;6.勾股定理

练习册系列答案
相关题目
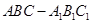 中,侧面
中,侧面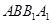 ,
,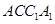 均为正方形,∠
均为正方形,∠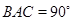 ,点
,点 是棱
是棱 的中点.
的中点.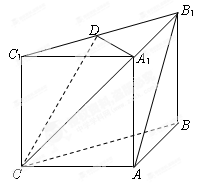
 ⊥平面
⊥平面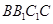 ;
;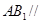 平面
平面 ;
;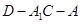 的余弦值.
的余弦值.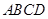 中,
中,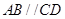 ,
,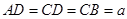 ,
,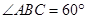 ,平面
,平面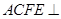 平面
平面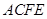 是矩形,
是矩形,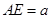 ,点
,点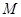 在线段EF上.
在线段EF上.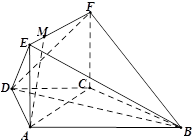
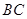 与
与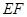 所成的角;
所成的角;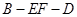 的余弦值.
的余弦值.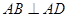 ,
,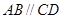 ,
,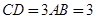 ,平面
,平面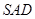 ⊥平面
⊥平面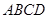 ,
, 是线段
是线段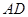 上一点,
上一点,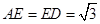 ,
,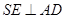 .
.
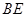 ⊥平面
⊥平面 ;
; ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.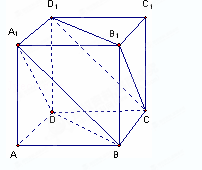
 ,AD=1.
,AD=1.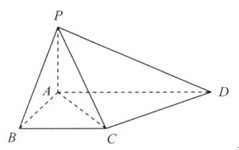
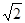 , BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.
, BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.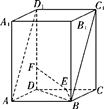
 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ ,
,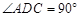 ,平面
,平面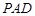 ⊥底面
⊥底面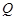 为
为 是棱
是棱 上的点,
上的点,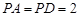 ,
,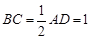 ,
,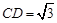 .
.
 ⊥平面
⊥平面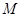 为棱
为棱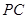 的中点,求异面直线
的中点,求异面直线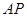 与
与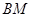 所成角的余弦值.
所成角的余弦值. 中,底面
中,底面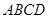 是正方形,侧面
是正方形,侧面 是正三角形,平面
是正三角形,平面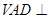 底面
底面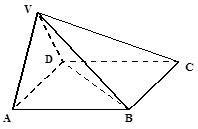
 为线段VC的中点,求证:
为线段VC的中点,求证: 平面
平面 ;
; 的体积.
的体积.