题目内容
【题目】设集合A={（x，y）|（x-4）2+y2=1}，B={（x，y）|（x-t）2+（y-at+2）2=1}，如果命题“t∈R，A∩B≠”是真命题，则实数a的取值范围是（ ）
A.
B.
C.
D.
,
【答案】B
【解析】
由题命题P：A∩B≠为真命题，再结合集合A、B的特征利用数形结合即可获得必要的条件，解不等式组即可获得问题的解答．
∵A={（x，y）|（x-4）2+y2=1}，表示平面坐标系中以M（4，0）为圆心，半径为1的圆，
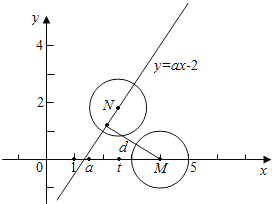
B={（x，y）|（x-t）2+（y-at+2）2=1}，表示以N（t，at-2）为圆心，半径为1的圆，且其圆心N在直线ax-y-2=0上，如图．
如果命题“t∈R，A∩B≠”是真命题，即两圆有公共点，则圆心M到直线ax-y-2=0的距离不大于2，
即
≤2，解得0≤a≤
．
∴实数a的取值范围是[0，]；
故选：B．
练习册系列答案
相关题目
