题目内容
(1)设函数f(x)=x2-1,对任意x∈[
,+∞),f(
)-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是
(2)函数f(x)=
,若方程f(x)=x+a恰有两个不等的实根,则a的取值范围是
| 3 |
| 2 |
| x |
| m |
(-∞,-
]∪[
,+∞)
| ||
| 2 |
| ||
| 2 |
(-∞,-
]∪[
,+∞)
.
| ||
| 2 |
| ||
| 2 |
(2)函数f(x)=
|
(-∞,1]
(-∞,1]
.分析:(1)将函数代入,再化简并分离参数,确定函数的最值,即可求得m的取值范围;
(2)在同一坐标系中画出函数f(x)的图象与函数y=x+a的图象,利用数形结合,易求出满足条件实数a的取值范围.
(2)在同一坐标系中画出函数f(x)的图象与函数y=x+a的图象,利用数形结合,易求出满足条件实数a的取值范围.
解答: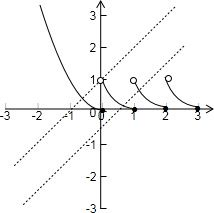 解:(1)把f(x)=x2-1代入,
解:(1)把f(x)=x2-1代入,
-1-4m2(x2-1)≤(x-1)2-1+4(m2-1)
化简分离参数,由x∈[
,+∞)可得
-4m2≤-
-
+1
令y=-
-
+1,由x∈[
,+∞)可得函数在由x∈[
,+∞)上单调递增,所以x=
时,y取得最小值为-
所以得
-4m2≤-
整理得:12m4-5m2-3≥0
所以(3m2+1)(4m2-3)≥0,所以4m2-3≥0
即m∈(-∞,-
]∪[
,+∞);
(2)函数f(x)=
的图象如图所示,
当a<1时,函数y=f(x)的图象与函数y=x+a的图象有两个交点,即方程f(x)=x+a有且只有两个不相等的实数根.
故答案为:(1)(-∞,-
]∪[
,+∞);
(2)(-∞,1]
 解:(1)把f(x)=x2-1代入,
解:(1)把f(x)=x2-1代入,| x2 |
| m2 |
化简分离参数,由x∈[
| 3 |
| 2 |
| 1 |
| m2 |
| 3 |
| x2 |
| 2 |
| x |
令y=-
| 3 |
| x2 |
| 2 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 8 |
| 3 |
所以得
| 1 |
| m2 |
| 8 |
| 3 |
整理得:12m4-5m2-3≥0
所以(3m2+1)(4m2-3)≥0,所以4m2-3≥0
即m∈(-∞,-
| ||
| 2 |
| ||
| 2 |
(2)函数f(x)=
|
当a<1时,函数y=f(x)的图象与函数y=x+a的图象有两个交点,即方程f(x)=x+a有且只有两个不相等的实数根.
故答案为:(1)(-∞,-
| ||
| 2 |
| ||
| 2 |
(2)(-∞,1]
点评:本题考查恒成立问题,考查方程根的研究,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目