题目内容
(2012•虹口区二模)已知:函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设函数f(x)=
.
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k•2x≥0在x∈[-1,1]时恒成立,求实数k的取值范围;
(3)如果关于x的方程f(|2x-1|)+t•(
-3)=0有三个相异的实数根,求实数t的取值范围.
| g(x) |
| x |
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k•2x≥0在x∈[-1,1]时恒成立,求实数k的取值范围;
(3)如果关于x的方程f(|2x-1|)+t•(
| 4 |
| |2x-1| |
分析:(1)根据函数g(x)=ax2-2ax+1+b(a≠0,b<1),可知函数在区间[2,3]上是单调函数,故可建立方程组,从而可求a、b的值及函数f(x)的解析式;
(2)利用分离参数法,求出函数的最值,即可得到结论;
(3)根据f(|2x-1|)+t•(
-3)=0,可得|2x-1|+
+
-3t-2=0,利用换元法u=|2x-1|>0,转化为u2-(3t+2)u+(4t+1)=0,当0<u1<1<u2时,原方程有三个相异实根,故可求实数t的取值范围.
(2)利用分离参数法,求出函数的最值,即可得到结论;
(3)根据f(|2x-1|)+t•(
| 4 |
| |2x-1| |
| 1 |
| |2x-1| |
| 4t |
| |2x-1| |
解答:解:(1)g(x)=ax2-2ax+1+b,函数的对称轴为直线x=1,由题意得:
①
得
②
得
(舍去)
∴a=1,b=0…(4分)
∴g(x)=x2-2x+1,f(x)=x+
-2…(5分)
(2)不等式f(2x)-k•2x≥0,即k≤(
)2-2•(
)+1…(9分)
设t=
,∴t∈[
,2],∴k≤(t-1)2
∵(t-1)2min=0,∴k≤0…(11分)
(3)f(|2x-1|)+t•(
-3)=0,即|2x-1|+
+
-3t-2=0.
令u=|2x-1|>0,则 u2-(3t+2)u+(4t+1)=0…(①…(13分)
记方程①的根为u1,u2,当0<u1<1<u2时,原方程有三个相异实根,
记φ(u)=u2-(3t+2)u+(4t+1),由题可知,
或
.…(16分)
∴-
<t<0时满足题设.…(18分)
①
|
|
②
|
|
∴a=1,b=0…(4分)
∴g(x)=x2-2x+1,f(x)=x+
| 1 |
| x |
(2)不等式f(2x)-k•2x≥0,即k≤(
| 1 |
| 2x |
| 1 |
| 2x |
设t=
| 1 |
| 2x |
| 1 |
| 2 |
∵(t-1)2min=0,∴k≤0…(11分)
(3)f(|2x-1|)+t•(
| 4 |
| |2x-1| |
| 1 |
| |2x-1| |
| 4t |
| |2x-1| |
令u=|2x-1|>0,则 u2-(3t+2)u+(4t+1)=0…(①…(13分)
记方程①的根为u1,u2,当0<u1<1<u2时,原方程有三个相异实根,
记φ(u)=u2-(3t+2)u+(4t+1),由题可知,
|
|
∴-
| 1 |
| 4 |
点评:本题考查函数的单调性,考查函数的最值,考查分离参数法求解恒成立问题,考查函数与方程思想,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
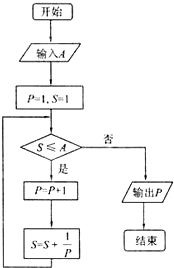 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为