题目内容
定义运算a*b为:a*b=
,例如1*2=1,2*1=1,设函数f(x)=sinx*cosx,则函数f(x)的最小正周期为
|
2π
2π
,使f(x)>0成立的集合为(2kπ,2kπ+
)
| π |
| 2 |
(2kπ,2kπ+
)
.| π |
| 2 |
分析:已知中a*b=
,易得f(x)=sinx*cosx的功能为计算sinx与cosx最小值,结合正弦函数和余弦函数的图象,分析即可得到答案.
|
解答:解:由已知中a*b=
可知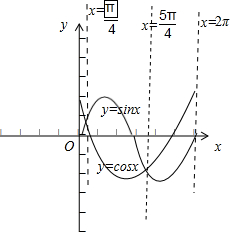
新运算的功能是计算a,b中的最小值,
则f(x)=sinx*cosx的功能为取sinx与cosx较小值,
由y=sinx与y=cosx的图象即可得函数f(x)的最小正周期为2π,f(x)>0成立的集合为(2kπ,2kπ+
)
故答案为:2π,(2kπ,2kπ+
).
|

新运算的功能是计算a,b中的最小值,
则f(x)=sinx*cosx的功能为取sinx与cosx较小值,
由y=sinx与y=cosx的图象即可得函数f(x)的最小正周期为2π,f(x)>0成立的集合为(2kπ,2kπ+
| π |
| 2 |
故答案为:2π,(2kπ,2kπ+
| π |
| 2 |
点评:本题考查的知识点是正弦函数和余弦函数的图象与性质,作图是关键,属于中档题.

练习册系列答案
相关题目