题目内容
已知函数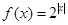 ,若存在
,若存在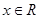 ,使得不等式
,使得不等式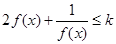 成立,则实数
成立,则实数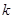 的最小值是( )
的最小值是( )
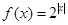 ,若存在
,若存在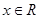 ,使得不等式
,使得不等式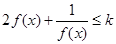 成立,则实数
成立,则实数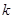 的最小值是( )
的最小值是( )| A.3 | B.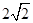 | C.2 | D.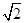 |
A
解:设F(x)=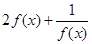 ,由于F(-x)=F(x),∴F(x)是偶函数,
,由于F(-x)=F(x),∴F(x)是偶函数,
当x≥0时,F(x)=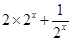 ,设x1>x2≥0,则F(x1)-F(x2)=
,设x1>x2≥0,则F(x1)-F(x2)=
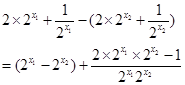
∵x1>x2≥0,∴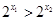 ,
,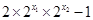 >0,∴F(x1)-F(x2)>0,
>0,∴F(x1)-F(x2)>0,
∴F(x)在[0,+∞)上是增函数,当x=0时,F(x)取得最小值3.
又F(x)是偶函数,其图象关于y轴对称,∴当x∈R时,F(x)取得最小值3.
∵存在实数x使得不等式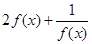 ≤k成立,∴k≥3,则实数k的最小值是3
≤k成立,∴k≥3,则实数k的最小值是3
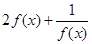 ,由于F(-x)=F(x),∴F(x)是偶函数,
,由于F(-x)=F(x),∴F(x)是偶函数,当x≥0时,F(x)=
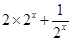 ,设x1>x2≥0,则F(x1)-F(x2)=
,设x1>x2≥0,则F(x1)-F(x2)=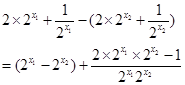
∵x1>x2≥0,∴
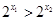 ,
,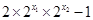 >0,∴F(x1)-F(x2)>0,
>0,∴F(x1)-F(x2)>0,∴F(x)在[0,+∞)上是增函数,当x=0时,F(x)取得最小值3.
又F(x)是偶函数,其图象关于y轴对称,∴当x∈R时,F(x)取得最小值3.
∵存在实数x使得不等式
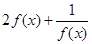 ≤k成立,∴k≥3,则实数k的最小值是3
≤k成立,∴k≥3,则实数k的最小值是3
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
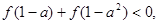 求实数a的取值范围
求实数a的取值范围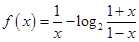 ,求函数的定义域,并判断它的奇偶性。
,求函数的定义域,并判断它的奇偶性。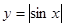 的一个单调增区间是( )
的一个单调增区间是( )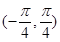
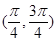
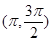
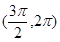
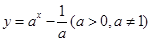 的图象可能是( )
的图象可能是( )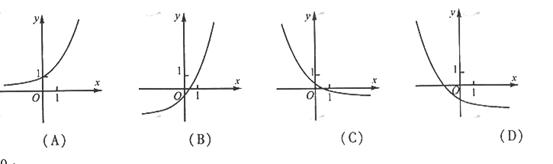
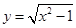
 的单调递减区间为________.
的单调递减区间为________.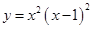 在区间(0,1)内( )
在区间(0,1)内( )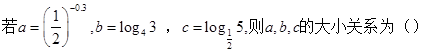
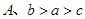
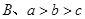
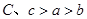
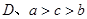
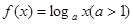 ,
,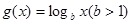 ,当
,当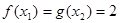 时,有
时,有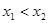 ,则
,则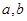 的大小关系是____________.
的大小关系是____________.