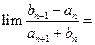题目内容
设等差数列{an}满足a3=5,a10=-9.
(1)求数列{an}的通项公式;
(2)求Sn的最大值及其相应的n的值.
(1)求数列{an}的通项公式;
(2)求Sn的最大值及其相应的n的值.
(1)由题意可得公差d=
=-2,
故数列{an}的通项公式为:an=5-2(n-3)=11-2n
(2)由(1)可得a1=9,
故Sn=9n+
×(-2)=10n-n2=-(n-5)2+25.
所以n=5时,Sn取得最大值
| a10-a3 |
| 10-3 |
故数列{an}的通项公式为:an=5-2(n-3)=11-2n
(2)由(1)可得a1=9,
故Sn=9n+
| n(n-1) |
| 2 |
所以n=5时,Sn取得最大值

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
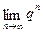 存在
存在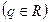 ,则
,则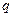 的取值范围是( )
的取值范围是( )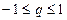 B
B 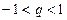 C
C 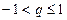 D
D 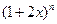 展开式的各项系数的和为
展开式的各项系数的和为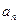 ,各二项式系数的和为
,各二项式系数的和为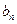 则
则