题目内容
【题目】设数列{an}满足an+1=an2﹣an+1(n∈N*),Sn为{an}的前n项和.证明:对任意n∈N* ,
(I)当0≤a1≤1时,0≤an≤1;
(II)当a1>1时,an>(a1﹣1)a1n﹣1;
(III)当a1= ![]() 时,n﹣
时,n﹣ ![]() <Sn<n.
<Sn<n.
【答案】证明:(Ⅰ)用数学归纳法证明. ①当n=1时,0≤an≤1成立.
②假设当n=k(k∈N*)时,0≤ak≤1,
则当n=k+1时, ![]() =(
=( ![]() )2+
)2+ ![]() ∈[
∈[ ![]() ][0,1],
][0,1],
由①②知, ![]() .
.
∴当0≤a1≤1时,0≤an≤1.
(Ⅱ)由an+1﹣an=( ![]() )﹣an=(an﹣1)2≥0,知an+1≥an .
)﹣an=(an﹣1)2≥0,知an+1≥an .
若a1>1,则an>1,(n∈N*),
从而 ![]() =
= ![]() ﹣an=an(an﹣1),
﹣an=an(an﹣1),
即 ![]() =an≥a1 ,
=an≥a1 ,
∴ ![]() ,
,
∴当a1>1时,an>(a1﹣1)a1n﹣1 .
(Ⅲ)当 ![]() 时,由(Ⅰ),0<an<1(n∈N*),故Sn<n,
时,由(Ⅰ),0<an<1(n∈N*),故Sn<n,
令bn=1﹣an(n∈N*),由(Ⅰ)(Ⅱ),bn>bn+1>0,(n∈N*),
由 ![]() ,得
,得 ![]() .
.
∴ ![]() =(b1﹣b2)+(b2﹣b3)+…+(bn﹣bn+1)=b1﹣bn+1<b1=
=(b1﹣b2)+(b2﹣b3)+…+(bn﹣bn+1)=b1﹣bn+1<b1= ![]() ,
,
∵ ![]() ≥
≥ ![]() ,
,
∴nbn2![]() ,即
,即 ![]() ,(n∈N*),
,(n∈N*),
∵ ![]() =
= ![]() =
= ![]() ,
,
∴b1+b2+…+bn![]() [(
[( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )]=
)]= ![]() ,
,
即n﹣Sn![]() ,亦即
,亦即 ![]() ,
,
∴当 ![]() 时,
时, ![]() .
.
【解析】(Ⅰ)用数学归纳法能证明当0≤a1≤1时,0≤an≤1.(Ⅱ)由an+1﹣an=( ![]() )﹣an=(an﹣1)2≥0,知an+1≥an . 从而
)﹣an=(an﹣1)2≥0,知an+1≥an . 从而 ![]() =an≥a1 , 由此能证明当a1>1时,an>(a1﹣1)a1n﹣1 . (Ⅲ)当
=an≥a1 , 由此能证明当a1>1时,an>(a1﹣1)a1n﹣1 . (Ⅲ)当 ![]() 时,Sn<n,令bn=1﹣an(n∈N*),则bn>bn+1>0,(n∈N*),由
时,Sn<n,令bn=1﹣an(n∈N*),则bn>bn+1>0,(n∈N*),由 ![]() ,得
,得 ![]() .从而
.从而 ![]() ,(n∈N*),由此能证明当
,(n∈N*),由此能证明当 ![]() 时,
时, ![]() .
.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系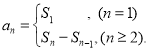 .
.

 阅读快车系列答案
阅读快车系列答案

