题目内容
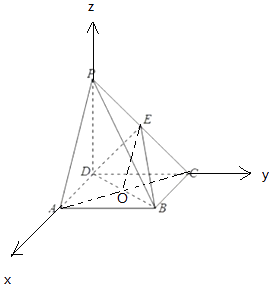
【题目】如图1,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC= ![]() CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥CD.
CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥CD. 
(Ⅰ)若E是PC的中点,求证:AP∥平面BDE;
(Ⅱ)求证:平面PCD⊥平面ABCD;
(Ⅲ)求二面角A﹣PB﹣C的大小.
【答案】证明:(Ⅰ)连接AC交BD于点O,连接OE, 在正方形ABCD中,O为AC的中点,又因为E为PC的中点,
所以OE为△PAC的中位线,
所以OE∥AP,
又因为OE平面BDE,AP平面BDE,
所以AP∥平面BDE.
(Ⅱ)由已知可得AD⊥PD,AD⊥CD,
又因为PD∩CD=D,PD,CD平面PCD,
所以AD⊥平面PCD,
又因为AD平面ABCD,
所以平面PCD⊥平面ABCD.
解:(Ⅲ)由(Ⅱ)知AD⊥平面PCD,所以AD⊥PD,又因为PD⊥CD,且AD∩CD=D,
所以PD⊥平面ABCD,
所以以D为坐标原点,DA,DC,DP所在直线分别为x,y,z轴,建立空间直角坐标系,
则P(0,0,2),A(2,0,0),B(2,2,0),C(0,2,0),
所以 ![]() ,
, ![]() ,
,
设平面APB的一个法向量为 ![]() ,
,
所以 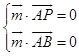 即
即 ![]()
令a=1,则c=1,从而 ![]() ,
,
同理可求得平面PBC的一个法向量为 ![]() ,
,
设二面角A﹣PB﹣C的大小为θ,易知 ![]() ,
,
所以 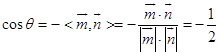 ,所以
,所以 ![]() ,
,
所以二面角A﹣PB﹣C的大小为 ![]() .
.
【解析】(Ⅰ)连接AC交BD于点O,连接OE,推导出OE∥AP,由此能证明AP∥平面BDE.(Ⅱ)推导出AD⊥PD,AD⊥CD,从而AD⊥平面PCD,由此能证明平面PCD⊥平面ABCD.(Ⅲ)以D为坐标原点,DA,DC,DP所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PB﹣C的大小.
【考点精析】利用直线与平面平行的判定和平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】甲、乙两人玩一种游戏,游戏规则如下:先将筹码放在如下表的正中间D处,投掷一枚质地均匀的硬币,若正面朝上,筹码向右移动一格;若反面朝上,筹码向左移动一格.
A | B | C | D | E | F | G |
30 | 5 | 10 | 10 | 5 | 20 | 30 |
(1)将硬币连续投掷三次,现约定:若筹码停在A或B或C或D处,则甲赢;否则,乙赢.问该约定对乙公平吗?请说明理由.
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定: ①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A﹣G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.