题目内容
设函数 .
.
(1)求函数 的图像在点
的图像在点 处的切线方程;
处的切线方程;
(2)求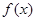 的单调区间;
的单调区间;
(3)若 ,
, 为整数,且当
为整数,且当 时,
时, ,求
,求 的最大值.
的最大值.
(1)函数 的图像在点
的图像在点 处的切线方程为
处的切线方程为 ;(2)若
;(2)若 ,
, 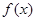 在区间
在区间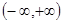 上单调递增,若
上单调递增,若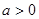 ,
,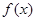 在区间
在区间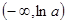 上单调递减,在
上单调递减,在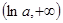 上单调递增;(3)整数
上单调递增;(3)整数 的最大值为2.
的最大值为2.
解析试题分析:(1)求函数 的图像在点
的图像在点 处的切线方程,只需求出斜率
处的切线方程,只需求出斜率 即可,由导数的几何意义可知,
即可,由导数的几何意义可知,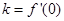 ,因此对函数
,因此对函数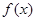 求导,得
求导,得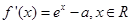 ,求出
,求出 的斜率,由点斜式可得切线方程;(2)求函数
的斜率,由点斜式可得切线方程;(2)求函数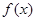 的单调区间,可先求出函数的导数
的单调区间,可先求出函数的导数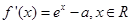 ,由于函数中含有字母
,由于函数中含有字母 ,故应按
,故应按 的取值范围进行分类讨论研究函数的单调性,给出单调区间;(3)由题设条件结合(2),将不等式,
的取值范围进行分类讨论研究函数的单调性,给出单调区间;(3)由题设条件结合(2),将不等式, 在
在 时成立转化为
时成立转化为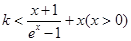 成立,由此问题转化为求
成立,由此问题转化为求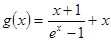 在
在 上的最小值问题,求导,确定出函数的最小值,即可得出
上的最小值问题,求导,确定出函数的最小值,即可得出 的最大值.本题解题的关键一是应用分类的讨论的方法,第二是化归思想,将问题转化为求函数的最小值问题.
的最大值.本题解题的关键一是应用分类的讨论的方法,第二是化归思想,将问题转化为求函数的最小值问题.
试题解析:(1)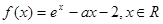 ,
,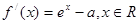 ,
,
函数 的图像在点
的图像在点 处的切线方程为
处的切线方程为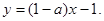
(2)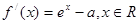 .
.
若 ,则
,则 恒成立,所以,
恒成立,所以,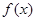 在区间
在区间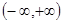 上单调递增.
上单调递增.
若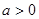 ,则当
,则当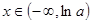 时,
时,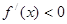 ,当
,当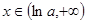 时,
时, ,
,
所以,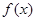 在区间
在区间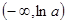 上单调递减,在
上单调递减,在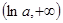 上单调递增.
上单调递增.
(3)由于 ,所以,
,所以,
故当 时,
时, ①
①
令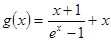 ,则
,则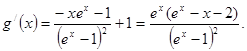
函数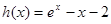 在
在 上单调递增,而
上单调递增,而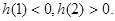
所以 在
在 上存在唯一的零点,故
上存在唯一的零点,故 在
在 上存在唯一的零点.
上存在唯一的零点.
设此零点为 ,则
,则 .当
.当 时,
时, ;当
;当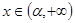 时,
时,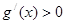 ;
;
所以,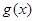 在
在 上的最小值为
上的最小值为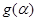 .由
.由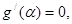 可得
可得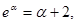
所以,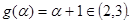 由于①式等价于
由于①式等价于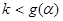 .
.
故整数 的最大值为2.
的最大值为2.
考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.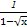 +
+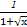 .
.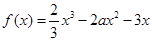 .
. 时,求曲线
时,求曲线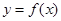 在点
在点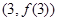 的切线方程;
的切线方程;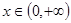 ,
,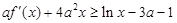 恒成立,求实数
恒成立,求实数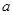 的取值范围;
的取值范围;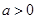 时,试讨论
时,试讨论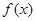 在
在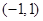 内的极值点的个数.
内的极值点的个数.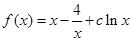 ,其中
,其中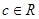 ,
,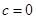 时,求曲线
时,求曲线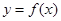 在点
在点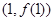 处的切线方程;
处的切线方程;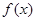 的单调性;
的单调性;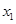 和
和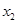 ,记过点
,记过点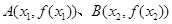 的直线的斜率为
的直线的斜率为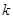 ,问是否存在
,问是否存在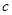 ,使得
,使得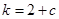 ?若存在,求出
?若存在,求出 +
+ 是否有实数解,并说明理由.
是否有实数解,并说明理由.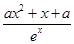 .
. 恒成立,求a的取值范围.
恒成立,求a的取值范围.