题目内容
已知数列{an}满足: ,
,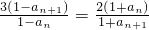 (n∈N*),数列{bn}=1-{an}2(n∈N*),数列{cn}={an+1}2-{an}2
(n∈N*),数列{bn}=1-{an}2(n∈N*),数列{cn}={an+1}2-{an}2
(n∈N*).
(1)证明数列{bn}是等比数列;
(2)求数列{cn}的通项公式;
(3)是否存在数列cn的不同项ci,cj,ck(i<j<k),使之成为等差数列?若存在请求出这样的不同项ci,cj,ck(i<j<k);若不存在,请说明理由.
解:(1)由已知an≠±1,bn≠0(n∈N*)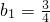 ,3(1-an+12)=2(1-an2)
,3(1-an+12)=2(1-an2)
an+12= +
+ an2,
an2,
所以{bn}是 为首项,
为首项, 为公比的等比数列
为公比的等比数列
(2)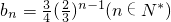
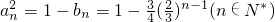
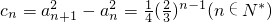
(3)假设存在ci,cj,ck满足题意成等差2cj=ci+ck代入得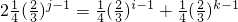
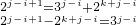 ,左偶右奇不可能成立.所以假设不成立,这样三项不存在.
,左偶右奇不可能成立.所以假设不成立,这样三项不存在.
分析:(1)由已知an≠±1,bn≠0,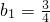 ,3(1-an+12)=2(1-an2),an+12=
,3(1-an+12)=2(1-an2),an+12= +
+ an2,
an2, ,由此能够证明数列{bn}是等比数列.
,由此能够证明数列{bn}是等比数列.
(2)由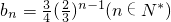 ,知
,知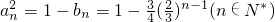 ,由此能求出{cn}的通项公式.
,由此能求出{cn}的通项公式.
(3)假设存在ci,cj,ck满足题意成等差2cj=ci+ck代入得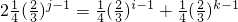 ,左偶右奇不可能成立.所以假设不成立,故这样三项不存在.
,左偶右奇不可能成立.所以假设不成立,故这样三项不存在.
点评:本题考查等比数列的证明、求解数列通项公式的方法和等差中项的综合运用,解题时要认真审题,仔细思考,注意合理地进行等价转化.
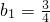 ,3(1-an+12)=2(1-an2)
,3(1-an+12)=2(1-an2)an+12=
 +
+ an2,
an2,
所以{bn}是
 为首项,
为首项, 为公比的等比数列
为公比的等比数列(2)
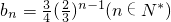
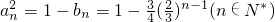
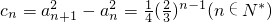
(3)假设存在ci,cj,ck满足题意成等差2cj=ci+ck代入得
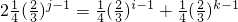
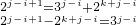 ,左偶右奇不可能成立.所以假设不成立,这样三项不存在.
,左偶右奇不可能成立.所以假设不成立,这样三项不存在.分析:(1)由已知an≠±1,bn≠0,
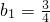 ,3(1-an+12)=2(1-an2),an+12=
,3(1-an+12)=2(1-an2),an+12= +
+ an2,
an2, ,由此能够证明数列{bn}是等比数列.
,由此能够证明数列{bn}是等比数列.(2)由
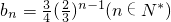 ,知
,知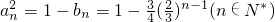 ,由此能求出{cn}的通项公式.
,由此能求出{cn}的通项公式.(3)假设存在ci,cj,ck满足题意成等差2cj=ci+ck代入得
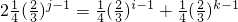 ,左偶右奇不可能成立.所以假设不成立,故这样三项不存在.
,左偶右奇不可能成立.所以假设不成立,故这样三项不存在.点评:本题考查等比数列的证明、求解数列通项公式的方法和等差中项的综合运用,解题时要认真审题,仔细思考,注意合理地进行等价转化.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目