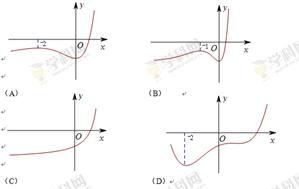
题目内容
已知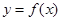 为R上的可导函数,当
为R上的可导函数,当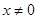 时,
时, 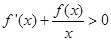 ,则函数
,则函数 的零点分数为( )
的零点分数为( )
| A.1 | B.2 | C.0 | D.0或2 |
C
解析试题分析:因为函数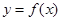 为R上的可导函数,当
为R上的可导函数,当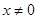 时,
时, 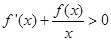 .即可
.即可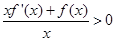 .令
.令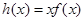 ,即
,即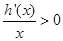 .所以可得
.所以可得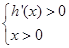 或
或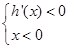 .所以当函数
.所以当函数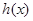 在
在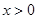 时单调递增,所以
时单调递增,所以 .即函数当
.即函数当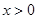 时,
时,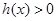 .同理
.同理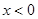 时,
时,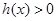 .又因为函数
.又因为函数 可化为
可化为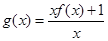 .所以当
.所以当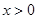 时,
时,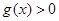 即与x轴没交点.当
即与x轴没交点.当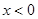 时,
时,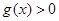 .所以函数
.所以函数 的零点个数为0.故选C.
的零点个数为0.故选C.
考点:1.函数的导数.2.函数的乘除的导数公式.3.函数的单调性.4.函数的最值.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
若函数
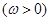 的图像在
的图像在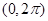 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则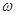 的取值范围是( )
的取值范围是( )
A.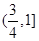 | B.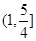 | C.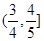 | D.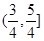 |
已知函数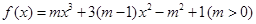 的单调递减区间是(0,4),则
的单调递减区间是(0,4),则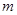 =( )
=( )
| A.3 | B. | C.2 | D.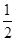 |
设函数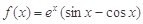
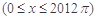 ,则函数
,则函数 的各极小值之和为 ( )
的各极小值之和为 ( )
A.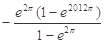 | B.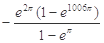 | C.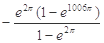 | D.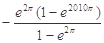 |
没函数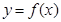 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数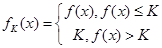 ,取函数
,取函数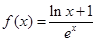 ,恒有
,恒有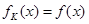 ,则
,则
A.K的最大值为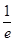 | B.K的最小值为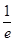 |
| C.K的最大值为2 | D.K的最小值为2 |
若点P是函数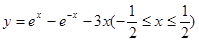 图象上任意一点,且在点P处切线的倾斜角为
图象上任意一点,且在点P处切线的倾斜角为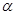 ,则
,则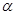 的最小值是( )
的最小值是( )
A. | B.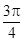 | C.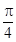 | D.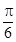 |
若曲线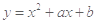 在点
在点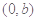 处的切线方程是
处的切线方程是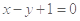 ,则 ( )
,则 ( )
A.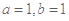 | B.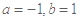 | C.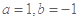 | D.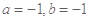 |
已知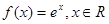 ,
,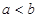 ,记
,记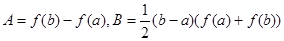 则
则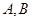 的大小关系是( )
的大小关系是( )
A.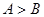 | B.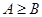 | C.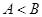 | D.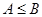 |
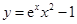 的部分图象为( )
的部分图象为( )