题目内容
若曲线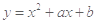 在点
在点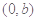 处的切线方程是
处的切线方程是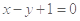 ,则 ( )
,则 ( )
A.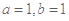 | B.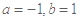 | C.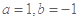 | D.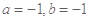 |
A
解析试题分析: 由导数知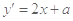 ,∴
,∴ 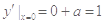 ∴
∴ ,∵
,∵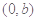 在切线
在切线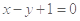 上,∴
上,∴ 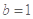 .
.
考点:导数的几何意义即求曲线上一点处的切线斜率.

练习册系列答案
相关题目
已知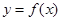 为R上的可导函数,当
为R上的可导函数,当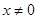 时,
时, 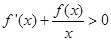 ,则函数
,则函数 的零点分数为( )
的零点分数为( )
| A.1 | B.2 | C.0 | D.0或2 |
已知函数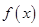 的定义域为
的定义域为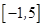 ,部分对应值如下表,
,部分对应值如下表,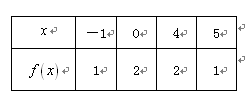
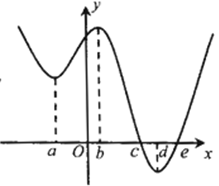
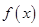 的导函数
的导函数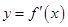 的图象如图所示.
的图象如图所示. 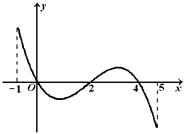
下列关于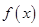 的命题:
的命题:
①函数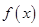 的极大值点为
的极大值点为 ,
,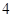 ;
;
②函数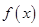 在
在 上是减函数;
上是减函数;
③如果当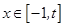 时,
时,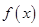 的最大值是2,那么
的最大值是2,那么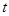 的最大值为4;
的最大值为4;
④函数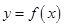 最多有2个零点.
最多有2个零点.
其中正确命题的序号是 ( )
| A.①② | B.③④ | C.①②④ | D.②③④. |
若 ,且函数
,且函数 在
在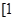 ,
, 上存在反函数,则( )
上存在反函数,则( )
A. | B. ∪ ∪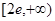 |
C. | D.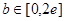 |
已知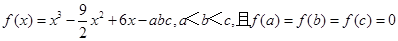 ,现给出如下结论:
,现给出如下结论:
①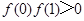 ;②
;②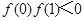 ;③
;③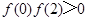 ;④
;④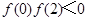 .
.
其中正确结论的序号为( )
| A.①③ | B.①④ | C.②④ | D.②③ |
设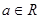 ,函数
,函数 的导函数为
的导函数为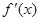 ,且
,且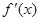 是奇函数,则
是奇函数,则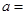 ( )
( )
| A.0 | B.1 | C.2 | D.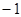 |
已知函数f(x)的导函数f′(x),且满足f(x)=2xf′(1)+ln x,则f′(1)=( ).
| A.-e | B.-1 | C.1 | D.e |

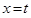 与函数
与函数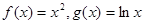 的图象分别交于点A、B,则|AB|的最小值为 ( )
的图象分别交于点A、B,则|AB|的最小值为 ( ) 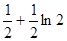 B.
B. C.
C. 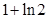 D.
D.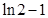
 ,其导函数
,其导函数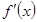 的图像如图所示,则下列叙述正确的是()
的图像如图所示,则下列叙述正确的是()