题目内容
已知函数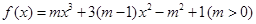 的单调递减区间是(0,4),则
的单调递减区间是(0,4),则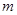 =( )
=( )
| A.3 | B. | C.2 | D.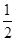 |
B
解析试题分析:由函数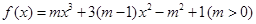 ,所以
,所以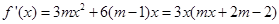 .令
.令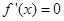 得
得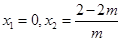 .又因为单调递减区间是(0, 4),所以可以得到
.又因为单调递减区间是(0, 4),所以可以得到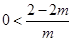 且
且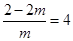 ,解得
,解得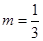 .故选B.
.故选B.
考点:1.函数的导数.2.函数的单调区间.3.含参数的数值的判定.

练习册系列答案
相关题目
.可导函数在闭区间的最大值必在( )取得
| A.极值点 | B.导数为0的点 |
| C.极值点或区间端点 | D.区间端点 |
等差数列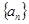 中的
中的 是函数
是函数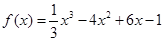 的极值点,则
的极值点,则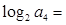 ( )
( )
A.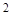 | B.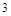 | C.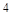 | D.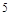 |
已知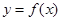 为R上的可导函数,当
为R上的可导函数,当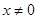 时,
时, 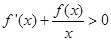 ,则函数
,则函数 的零点分数为( )
的零点分数为( )
| A.1 | B.2 | C.0 | D.0或2 |
已知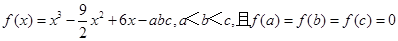 ,现给出如下结论:
,现给出如下结论:
①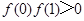 ;②
;②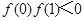 ;③
;③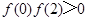 ;④
;④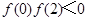 .
.
其中正确结论的序号为( )
| A.①③ | B.①④ | C.②④ | D.②③ |
若函数f(x)=x3-3x在(a,6-a2)上有最小值,则实数a的取值范围是( )
A.(-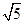 ,1) ,1) | B.[-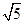 ,1) ,1) |
| C.[-2,1) | D.(-2,1) |
已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则 ( ).
| A.当k=1时,f(x)在x=1处取到极小值 |
| B.当k=1时,f(x)在x=1处取到极大值 |
| C.当k=2时,f(x)在x=1处取到极小值 |
| D.当k=2时,f(x)在x=1处取到极大值 |
已知函数f(x)的导函数f′(x),且满足f(x)=2xf′(1)+ln x,则f′(1)=( ).
| A.-e | B.-1 | C.1 | D.e |
直线y=kx+b与曲线y=x3+ax+1相切于点(2,3),则b的值为( ).
| A.-3 | B.9 | C.-15 | D.-7 |